Na boku
Piko: Na boku AB trójkąta ABC obrano punkt D taki że trójkąty ABC, ACD, CBD są podobne. Udowodnij że
trójkąt ABC jest prostokątny.
27 lut 20:26
Piko: ?
27 lut 20:42
Tadeusz:
baw się kątami
27 lut 20:52
Piko: Bawię się, ale nie wiem, czy od razu mogę założyć, że wszystkie trójkąty mają kąty proste. I
nie wiem czy wystarczy podać stosunek boków, czy trzeba to jakoś wyliczyć. Wg mnie najlepsza
zasada będzie bkb.
27 lut 20:57
Tadeusz:
... te trójkąty są podobne a nie przystające ... więc co tu ma bkb
27 lut 21:00
Piko: Bardzo dużo: cechy przystawania trójkątów, zasada bkb: Jeżeli dwa boki jednego trójkąta są
proporcjonalne do dwóch boków drugiego trójkąta i kąty zawarte między tymi bokami są równe, to
trójkąty są podobne.
27 lut 21:07
Tadeusz:
... pomieszanie z poplątaniem
Poczytaj co znaczy podobne a co przystające
27 lut 21:10
Piko: Mam Ci wysłać link do tego tekstu prosto z CKE?
27 lut 21:12
Tadeusz:
lepiej dokładnie go przeczytaj
27 lut 21:13
27 lut 21:14
Piko: A czego Ty tu niby nie rozumiesz?
27 lut 21:14
Tadeusz:
człowieku ... Ty nie odróżniasz przystawania od podobieństwa
i włącz wreszcie mózg
27 lut 21:16
Piko: przystawanie: bkb: dwa boki i zawarty kąt między nimi są RÓWNE
podobieństwo: dwa boki jednego trójkąta są PROPORCJONALNE do dwóch boków drugiego trójkąta, a
kąty między tymi bokami są RÓWNE
widzisz różnicę?
PS Ja do Ciebie mówię spokojnie, więc się uspokój, bo to nie na miejscu
27 lut 21:19
Tadeusz:
zacytuję Ci ca napisałeś o 21:07
"cechy przystawania trójkątów, zasada bkb: Jeżeli dwa boki jednego trójkąta
są proporcjonalne do dwóch boków drugiego trójkąta i kąty zawarte między tymi bokami
są równe, to trójkąty są podobne.
Czytaj co piszesz i co piszą do Ciebie ... jeśli nie to bańki nie zawracaj
27 lut 21:25
Piko: pomyliłem się, ale nie rozumiem Twojego pierwszego pytania (cytuję):
"Tadeusz: ... te trójkąty są podobne a nie przystające ... więc co tu ma bkb
"
i staram Ci wytłumaczyć, że jest taka zasada bkb
27 lut 21:28
Tadeusz:
a ja usiłuję Ci wytłumaczyć, że skoro wszystkie te trójkąty mają być podobne
to takiego samego boku nijak mieć nie mogą
27 lut 21:31
Piko: a czy ja powiedziałem, że mają mieć TAKI SAM bok? Cały czas piszę, że boki mają być
proporcjonalne. A kąt równy.
27 lut 21:32
Tadeusz:
a jak TY w dowolnym trójkącie masz zamiar szukać proporcji boków
?
27 lut 21:34
Tadeusz:
a najważniejsze: zasada kbk to takie same kąty i bok między nimi zawarty
TAKIE SAME
!
27 lut 21:35
Qulka: jeden pisze o bkb a drugi o kbk a tak w ogóle słyszałam że będzie to z kkk ;>
27 lut 21:38
Piko: Np. w tym zadaniu trójkąty ABC i BCD są podobne, bo |BC|/|AC|=|BD|/|CD| i kąt prosty między
tymi bokami
27 lut 21:39
Piko: Qulka tak będzie dobrze jak wytłumaczę i podam zasadę bkb i do tego dorzucę jeszcze trzeci
trójkąt ACD?
27 lut 21:40
Qulka: jak mi narysujesz to przeanalizuję
na sucho to nie wiem
27 lut 21:42
Tadeusz:
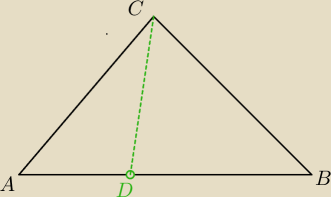
Narysowałem dowolny trójkąt ABC ... obrałem punkt D ... widzisz tu jakieś trójkąty podobne
27 lut 21:44
Piko:
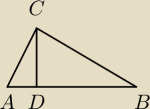
Tak to widzę
Ale nie wiem czy od razu mogę zakładać, że tam są kąty proste?
27 lut 21:44
Piko: Tadeusz: Ale w zadaniu jest, że dobrano taki punkt D, że trójkąty ABC, ACD i CBD są podobne.
Źle obrałeś punkt D w takim razie.
27 lut 21:45
Tadeusz:
Tak to widzisz .... i dobrze widzisz ...ale TY masz to udowodnić.
Dlatego piszę Ci "baw się kątami"
Skoro wszystkie te trójkąty mają być podobne to wszystkie mają takie same kąty jak
trójkąt ABC
27 lut 21:50
Piko: tak też można, owszem
są trzy zasady, a że wybrałem bkb nie musi oznaczać, że jest to zły
tok myślenia
27 lut 21:51
Tadeusz:
W dowolnym trójkącie ostrokątnym nijak tego punktu nie dobierzesz
Ustawiaj go na moim rysunku jak chcesz a zawsze punkt D będzie wierzchołkiem
dwóch kątów przyległych (jeden ostry drugi rozwarty ... chyba, że oba proste)
... i to byłoby prawie na tyle−
27 lut 21:55
Piko: ok, rozumiem
to wystarczy, że napiszę, że te wszystkie kąty są sobie równe i już?
27 lut 21:57
Tadeusz:
NIE
27 lut 21:59
Piko: No więc jak mam to zrobić czy ktoś mi w końcu powie?
27 lut 22:00
H3H3:
27 lut 22:01
Tadeusz:
Czytaj treść zadania
27 lut 22:02
Piko: Dobra, po co się wypowiadasz, jak nie zamierzasz pomóc? Tego to już w ogóle nie rozumiem.
Jakbym nie wiedział, że mam przeczytać zadanie....
27 lut 22:05
Tadeusz:
TYLKO NA PRZCIWPROSTOKĄTNEJ MOŻESZ OBRAĆ TAKI PUNKT D, ŻE
TRÓJKĄTY ABC ACD I BCD BĘDĄ PODOBNE. PUNKT D WYZNACZY WTEDY
WYSOKOŚĆ OPUSZCZONA Z WIERZCHOŁKA C
27 lut 22:06
Tadeusz:
JUŻ SIĘ NIE WYPOWIADAM .... BO TY NIE MYŚLISZ
BYE
27 lut 22:07
Piko: nie ubliżaj mi człowieku, bo nie jestem debilem i nie mam z matmy 1, ani 2, ani 3, ani 4 i
wyobraź sobie, że mogę nie rozumieć jednego zadania na tysiąc
27 lut 22:08
Mila:
Oj, Piko, właśnie otrzymujesz pomoc wysokiej jakości.
Gotowe rozwiązanie przeczytasz i zapomnisz.
27 lut 22:09
Piko: No dokładnie, a chciałbym to zrozumieć
27 lut 22:10
Qulka: Piko to kombinuj do rysunku z kątami, a nie sprzeczasz się o regułki
i wymyślasz
uogólnione teorie
27 lut 22:15
Qulka: jak będziesz próbował rozwiązać to będzie pomoc i wyjaśnienie..jak próbujecie wykazać sobie
który ma rację to nie ma o czym rozmawiać
27 lut 22:16
Piko: Dobra dzięki, miłej nocy Wam życzę
27 lut 22:18
Piko: Próbowałem z bkb, ale skoro źle, to już nie wiem
27 lut 22:19
Mila:
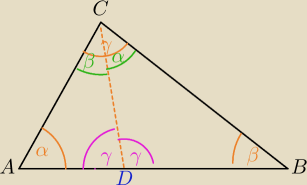
ΔACD∼ΔCBD to odpowiednie kąty jednego Δ są równe kątom drugiego,
to np. tak : zaznaczam na zielono kąty równe α i β, wtedy różowe kąty są równe γ⇔
2γ=180
o⇔γ=90
o
Inny wariant nie wchodzi w rachubę.
Możesz w podobny sposób inne warianty i dojść do sprzeczności.
27 lut 22:29
Piko: Dziękuję bardzo Mila!
Wszystko jasne!
27 lut 22:30
Qulka: jak próbowałeś z jednego i Ci mówią ze źle to szukaj innego sposobu , a nie fochy stroisz
i
nadal upierasz się przy jednym pomyśle
27 lut 22:31
Mila:
27 lut 22:33