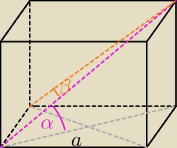
Wyznacz pole powierzchni... Kraterek: Dany jest prostopadłościan, którego dłuższa krawędź podstawy ma długość a. Jego przekątna jest nachylona do podstawy pod kątem α. Przekątna ta tworzy ze ścianą boczną, zawierającą dłuższą krawędź podstawy, kąt β. Wyznacz pole powierzchni bocznej walca opisanego na tym prostopadłościanie, jeśli krawędź boczna prostopadłościanu jest wysokością walca. Czy ktoś ma jakiś pomysł? Próbowałam na różne sposoby, ale nie wyszło.

J: wydaje mi się ( może niesłusznie ), że jest mało danych . Czy nie jest napisane: przekątna ( np.d )?

ax: banał−

J: ciekawe co dalej ? ( mając dane tylko a)

Tadeusz: a co tu ciekawego ? Jeśli jako H oznaczę wysokość prostopadłościanu i jako d przekątną prostopadłościanu to:

H
	=sinα
d

√H2+a2
	=cosβ
d

	H		sinα
czyli:		=
	√H2+a2		cosβ

Z tego wyznaczę H Mając H wyznaczę przekątną podstawy a przekątna podstawy jest średnicą walca opisanego ... i to by było na tyle −

J: zgoda

Tadeusz: ... jak zgoda to "Borys Polewoj" −

J:

Kraterek: J, dane dokładnie jak w treści zadania. ax, czy coś tu nie tak z tym rysunkiem, czy kąt β jest kątem pomiędzy przekątną bryły a przekątną ściany bocznej? (tu niewyraźnie widać) Tak właśnie powinno być.

	d
Wtedy cosβ =
	√H2+a2

Jednak może tak czy inaczej to wyjdzie.

J: rysunek jest dobry

Tadeusz: ... i tak to jest z Kraterkiem ... nigdy nie usłyszałem słowa thx −:(

Kraterek: Tadeusz, proszę o konkretny przykład (link) do sytuacji, gdy ktoś mi pomógł i nie otrzymał podziękowań. Problem polega na tym, że nie mam zwyczaju rozpływać się w podziękowaniach, dopóki problem nie jest do końca rozwiązany. A niestety nie jest. W Twojej podpowiedzi jest również błąd. Nie jest rozwiązany, ponieważ wyznaczenie przekątnej podstawy wymaga policzenia b², co jest możliwe, choć nieco skomplikowane. W każdym razie DZIĘKUJĘ bardzo za inspirację, podpowiedź się przydała, choć po korektach. No i czekam na przykłady tego "nigdy"

Tadeusz: Tobie wszyscy źle podpowiadają (rozwiązują) tak że ty biedna musisz po kimś poprawiać ... korygować ... ale wspaniałomyślnie dzięki za chęci https://matematykaszkolna.pl/forum/280791.html A w tym (bieżącym przykładzie błąd też jest "wydumany" przez Ciebie. To b² nie jest do niczego potrzebne ... chyba nie czytasz co Ci inni piszą albo nie zastanawiasz się nad tym. I to byłoby na tyle