Odcinek o końcach, jednokładność
ppawzik: Odcinek o końcach (3,−6) i D(7,2) jest obrazem odcinka o końcach A(−1,−4) i B(1,0) w pewnej
jednokładności o skali k. Wyznacz tę skalę oraz środek jednokładności P, jeśli k jest liczbą:
a) dodatnią b) ujemną
Bardzo proszę o pomoc

26 lut 20:48
Mila:
A spojrzysz na rozwiązanie, bo sporo pisania i nie chcę na darmo marnowac czasu.
26 lut 21:39
ppawzik: Niestety nie mam odpowiedzi

jestem pewien iż jest to ze zbioru zadań NE jednak dostaje tylko
kserówki zbiorów od nauczyciela
26 lut 22:41
Mila:
Chodziło mi o moje rozwiązanie, nie odpowiedź.
Już piszę.
26 lut 22:42
Qulka:
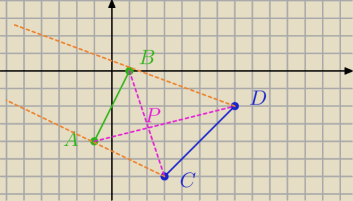
pomarańczowe k(+)
różowe k(−)
P1 to przecięcie się AC i AB (w pierwszym przypadku)
P2 to przecięcie się AD i BC (w drugim przypadku)
26 lut 22:46
Qulka: już widzę czemu brzydkie

D mam za nisko

26 lut 22:47
Qulka:
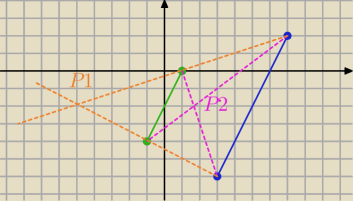
P1( −6−2) k=2
P2 (5/3 ; −2) k=−3
26 lut 22:51
Qulka: k=−2 w drugim

26 lut 22:51
ppawzik: Przepraszam, źle zrozumiałem jednak jestem w kropce zakończyłem zadanie na tym iż obliczyłem
wszystkie punkty: A(−1,−4) B(1,0) C(3,−6) D(7,2). Narysowałem wykres (jak powyżej za wyjątkiem
D) i napisałem równanie prostej AD y=6/8x+26/8 (dziwne jakieś te liczby mi wyszły) i
zastanawiam się co dalej...
26 lut 22:52
ppawzik: A czy mogłabyś wyjaśnić mi jak się oblicza tą jednokładność? Ponieważ nie do końca rozumiem na
czym to polega 'jak to się je'

26 lut 22:53
ppawzik: i dziękuje bardzo za rozwiązanie

26 lut 22:53
Qulka: przecięcie AD i BC daje Ci punkt P2 ale masz błąd (zły znak) bo AD to y=3/4 x − 13/4
26 lut 22:55
Qulka: Mila Ci pisze dokładne rozwiązanie bo ja to wszystko odczytuję z obrazków..poczekaj na nią

jednokładność to inaczej; świecenie latarką z jednego miejsca i oglądanie coraz większego
cienia na ścianie zależnie gdzie masz przedmiot

0 i ile razy cień jest większy to taka jest
skala jednokładności
26 lut 22:57
Mila:
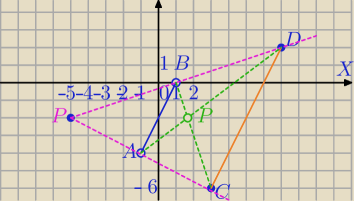
P=(x
s,y
s) −wsp. środka jednokładności
a) k>0⇔
Obrazem punktu A jest punkt C, obrzaem punktu B jest punkt D
|AB|=
√22+42=
√20
|CD|=
√42+82=
√80=2
√20
k=2
Z definicji jednokladności:
C(3,−6) i D(7,2) jest obrazem odcinka o końcach A(−1,−4) i B(1,0)
PC
→=2*PA
→⇔[3−x
s,−6−y
s]=2*[−1−x
s,−4−y
s]⇔
3−x
s=−2−2x
s⇔x
s=−5
−6−y
s=−8−2y
s⇔y
s=−2
[N[P=(−5,−2) środek jednokładności, k=2
PD
→=2*PB
→ Przelicz, czy otrzymasz to samo.
II sposób
Gdy ustaliłeś, k=2
Piszesz równanie prostej BD i prostej AC, punkt przecięcia prostych to P− środek jednokładności
b) k=−2 skala ujemna
Zmienia się to, że obrazem punktu A jest punkt D,
Obrazem punktu B jest punkt C
P'C
→(−2)*PB
→⇔[3−x
s,−6−y
s]=(−2)*[1−x
s,0−y
s]
[3−x
s,−6−y
s]=[−2+2x
s,2y
s]
3−x
s=−2+2x
s⇔5=3x
s
−6−y
s=2y
s⇔3y
s=−6
y
s=−2
II sposób po ustaleniu, że k=−2
piszesz równania prostych BC i AD, punkt przecięcia prostych to P− środek jednokładności.
26 lut 23:13
Qulka: Mila jesteś niesamowita

tyle pisania

podziwiam

26 lut 23:16
Qulka: a ja zrobiłam błąd licząc kratki

26 lut 23:17
Patryk: Przepraszam, że offtop, ale Mila mogłabyś?
281859
26 lut 23:18
Mila:
Mam nadzieję, że Pawik skorzysta.
26 lut 23:25
Qulka: pisałam mu żeby poczekał na Ciebie .. zobaczymy czy zajrzy
26 lut 23:30
Patryk: Jeśli nie to i tak u mnie wisi w zakładkach, bo fajnie wytłumaczone, więc wasza robota się nie
zmarnuje

27 lut 18:01
gorki: W internecie (prawie) nic nie ginie. Jeśli osoba pytająca nie skorzysta, to zrobią to "przyszłe
pokolenia"

26 kwi 02:50

 jestem pewien iż jest to ze zbioru zadań NE jednak dostaje tylko
kserówki zbiorów od nauczyciela
jestem pewien iż jest to ze zbioru zadań NE jednak dostaje tylko
kserówki zbiorów od nauczyciela
 pomarańczowe k(+)
różowe k(−)
P1 to przecięcie się AC i AB (w pierwszym przypadku)
P2 to przecięcie się AD i BC (w drugim przypadku)
pomarańczowe k(+)
różowe k(−)
P1 to przecięcie się AC i AB (w pierwszym przypadku)
P2 to przecięcie się AD i BC (w drugim przypadku)
 D mam za nisko
D mam za nisko 
 P1( −6−2) k=2
P2 (5/3 ; −2) k=−3
P1( −6−2) k=2
P2 (5/3 ; −2) k=−3



 jednokładność to inaczej; świecenie latarką z jednego miejsca i oglądanie coraz większego
cienia na ścianie zależnie gdzie masz przedmiot
jednokładność to inaczej; świecenie latarką z jednego miejsca i oglądanie coraz większego
cienia na ścianie zależnie gdzie masz przedmiot  0 i ile razy cień jest większy to taka jest
skala jednokładności
0 i ile razy cień jest większy to taka jest
skala jednokładności
 P=(xs,ys) −wsp. środka jednokładności
a) k>0⇔
Obrazem punktu A jest punkt C, obrzaem punktu B jest punkt D
|AB|=√22+42=√20
|CD|=√42+82=√80=2√20
P=(xs,ys) −wsp. środka jednokładności
a) k>0⇔
Obrazem punktu A jest punkt C, obrzaem punktu B jest punkt D
|AB|=√22+42=√20
|CD|=√42+82=√80=2√20
 tyle pisania
tyle pisania  podziwiam
podziwiam 


