Stereometria - ostrosłup
Patryk: Podstawą ostrosłupa jest trójkąt o kątach 30 i 45 stopni przyległych do boku o długości 8.
Spodek wysokości jest środkiem okręgu wpisanego w podstawę, a krawędź boczna jest nachylona do
płaszczyzny podstawy pod kątem 60 stopni. Oblicz dokładną objętość ostrosłupa.
Z tw. Sinusów obliczyłem 2 bok podstawy, po czym obliczyłem pole podstawy, ale to by było na
tyle.
Jak będzie wyglądał rzut krawędzi bocznej na podstawę? Będzie się zawierał w wysokości podstawy
− trójkąta? Jak obliczyć wysokość ostrosłupa?
26 lut 19:56
dero2005:
oblicz promień r okręgu wpisanego w trójkąt podstawy
26 lut 20:52
Mila:
Dero, to nie będzie dobrze.
Patryk dobrze zapisałeś treść?
Może ściana boczna jest nachylona do podstawy pod kątem 60 o.
26 lut 20:57
dero2005:
Rzeczywiście, ja odczytałem ( pewnie w wyobraźni), że ściana boczna jest pochylona pod kątem
60
o
26 lut 21:12
dero2005:
Przecież jeżeli spodek wysokości jest w środku okręgu wpisanego to musi chodzic o ściane boczną
26 lut 21:16
Mila:
Też tak myślę.Poczekamy co napisze Patryk.
26 lut 21:19
Patryk: Już jestem, film oglądałem.
Tak, treść jest poprawnie przepisana, lecz... nie wiem czemu w odpowiedzi jest krok (po
obliczeniu krawędzi podstawy) następujący:
Wyznaczenie długości promienia okręgu opisanego na podstawie i wyznaczenie wysokości
ostrosłupa.
Dlatego się pytam, bo coś mi tu nie gra

26 lut 22:40
Patryk: Czyli rozumiem, że może być błąd w treści?
26 lut 22:42
Mila:
A jaka jest odpowiedź? (wynik).
Może z niej domyślę się o co chodzi.
26 lut 23:24
26 lut 23:26
Mila:
Jutro policzę
Patryku, jeśli wcześniej
Dero ( wielki specjalista ze stereometrii) nie
napisze.
Za chwilę idę spać. Dobranoc

26 lut 23:31
Patryk: Będę czekał i dziękuję

Również życzę dobrej nocy

26 lut 23:33
dero2005:
Z treści zadania wynika że:
− podstawa jest trójkątem nierównobocznym
− spodek wysokości pokrywa się ze środkiem okręgu wpisanego w podstawę (z tego wniosek, że
wysokości ścian bocznych są równe i jednakowo pochylona)
− krawędź boczna jest pochylona do podstawy pod kątem 60
o ( pytanie, która krawędź, są trzy
każda pochylona pod innym kątem)

?
27 lut 09:19
dero2005:
Jeżeli przyjąć, że spodek wysokości jest środkiem okręgu opisanego na trójkącie podstawy to
objętość wyjdzie jak w odpowiedzi ):
27 lut 11:55
Patryk: Czyli źle sfornuowana treść

powinno być, że ten kąt to kąt między ścianą boczną a podstawą.
Wielkie dzięki dero za sprawdzenie tego, pozdrawiam

27 lut 13:47
dero2005:
Powinno być, że spodek wysokości jest środkiem okręgu opisanego a nie wpisanego.
27 lut 13:54
Patryk: Okej, dzięki

A tak swoją drogą zrobiłbyś te zadanie
281863? Bo próbowałem rozwiązać i mi nie wyszło, a
z racji, że uczę się stereometrii, to zaciekawiło mnie

27 lut 14:42
Mila:
Wg propozycji Dero z godziny 13:54 wynik jak w odpowiedzi.
Licz Patryk. Jeśli nie otrzymasz dobrego wyniku po 20 napiszę.
27 lut 15:56
Patryk: Udało się

Jeszcze raz dzięki.
Mila, chciałoby ci się pobawić z tym zadaniem, co wyżej dałem link? Mógłbym napisać mój
tok rozumowania, ale niestety nie do końca jest poprawny, gdyż nie wychodzi mi wynik taki,
jaki powinien.
27 lut 19:13
prosta: myślę, że będę mogła pomóc
27 lut 19:18
Patryk: Hmm, no to poczaruję z rysunkiem

27 lut 19:25
Patryk:
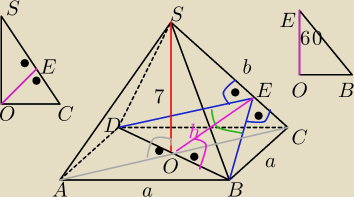
A więc treść:
Dany jest ostrosłup prawidłowy czworokątny o wysokości 7, w którym kąt między sąsiednimi
ścianami bocznymi ma miarę 120 stopni.
Wynik ma wyjść 14.
∡DEB=120
H=7
|SC| = b
|OE| = h
|AB| = a
|AC| = 2
√2
A więc wziąłem sobie trójkąt OCS do obliczeń.
|OC| − połowa przekątnej podstawy, czyli
Ze wzoru na pole trójkąta mamy
| 1 | | 1 | | a√2 | |
| * h * b = |
| * 7 * |
| |
| 2 | | 2 | | 2 | |
długość b sobie wyznaczam z pitagorasa na tym trójkącie:
Wyliczone b podstawiam do wcześniejszego wzoru na h
2
Mając odległość h (|OE) możemy wykorzystać informacje o kącie 120 stopni, czyli weźmy trójkąt
OBE, który jest prostokątny i przy wierzchołku E jest kąt 60 stopni.
tg 60 =
√3
√2a2 + 196=2
√3
No i dalej obustronnie podnosząc do kwadratu wychodzi mi tak, że a
2 < 0 :C
Więc o co chodzi?

27 lut 19:53
Patryk: No i dodam, że jak się podstawi wynik pod a, to się nie zgadza (wychodzi 7=1), czyli po drodze
musiałem coś pochrzanić.
27 lut 19:59
prosta: przedostatnia linijka.....przez 14 zamiast przez 2
27 lut 20:10
prosta: i wszystko pasuje

27 lut 20:12
prosta: ja moje rozwiązanie opieram na podobieństwie trójkątów: OCS i OCE....nie muszą wtedy liczyć b.
27 lut 20:13
Patryk: Taki banalny błąd na finiszu... Wielkie dzięki!

Tak wiem o co chodzi, też tak wcześniej próbowałem, ale tez gdzieś błąd popełniałem.
Tyle liczenia i kombinowania, żeby walnąć się na 7 * 2...
Dzięki i pozdrawiam!

27 lut 20:19
Mila:
Widzę, że wszystko rozwiązane. Byłam dość zajęta do tej pory.

27 lut 20:37
Patryk: Dzięki, ze przynajmniej zajrzałaś

27 lut 20:44
Mila:

27 lut 21:27



 Również życzę dobrej nocy
Również życzę dobrej nocy 
 ?
?
 powinno być, że ten kąt to kąt między ścianą boczną a podstawą.
Wielkie dzięki dero za sprawdzenie tego, pozdrawiam
powinno być, że ten kąt to kąt między ścianą boczną a podstawą.
Wielkie dzięki dero za sprawdzenie tego, pozdrawiam 
 A tak swoją drogą zrobiłbyś te zadanie 281863? Bo próbowałem rozwiązać i mi nie wyszło, a
z racji, że uczę się stereometrii, to zaciekawiło mnie
A tak swoją drogą zrobiłbyś te zadanie 281863? Bo próbowałem rozwiązać i mi nie wyszło, a
z racji, że uczę się stereometrii, to zaciekawiło mnie 
 Jeszcze raz dzięki.
Mila, chciałoby ci się pobawić z tym zadaniem, co wyżej dałem link? Mógłbym napisać mój
tok rozumowania, ale niestety nie do końca jest poprawny, gdyż nie wychodzi mi wynik taki,
jaki powinien.
Jeszcze raz dzięki.
Mila, chciałoby ci się pobawić z tym zadaniem, co wyżej dałem link? Mógłbym napisać mój
tok rozumowania, ale niestety nie do końca jest poprawny, gdyż nie wychodzi mi wynik taki,
jaki powinien.

 A więc treść:
Dany jest ostrosłup prawidłowy czworokątny o wysokości 7, w którym kąt między sąsiednimi
ścianami bocznymi ma miarę 120 stopni.
Wynik ma wyjść 14.
∡DEB=120
H=7
|SC| = b
|OE| = h
|AB| = a
|AC| = 2√2
A więc wziąłem sobie trójkąt OCS do obliczeń.
|OC| − połowa przekątnej podstawy, czyli
A więc treść:
Dany jest ostrosłup prawidłowy czworokątny o wysokości 7, w którym kąt między sąsiednimi
ścianami bocznymi ma miarę 120 stopni.
Wynik ma wyjść 14.
∡DEB=120
H=7
|SC| = b
|OE| = h
|AB| = a
|AC| = 2√2
A więc wziąłem sobie trójkąt OCS do obliczeń.
|OC| − połowa przekątnej podstawy, czyli


 Tak wiem o co chodzi, też tak wcześniej próbowałem, ale tez gdzieś błąd popełniałem.
Tyle liczenia i kombinowania, żeby walnąć się na 7 * 2...
Dzięki i pozdrawiam!
Tak wiem o co chodzi, też tak wcześniej próbowałem, ale tez gdzieś błąd popełniałem.
Tyle liczenia i kombinowania, żeby walnąć się na 7 * 2...
Dzięki i pozdrawiam! 


