Planimetria xyz: 2. Wysokości równoległoboku wynoszą 2,4cm i 4cm a jego obwód jest równy 16cm Oblicz cosinus kąta rozwartego między przekątnymi tego równoległoboku. Obliczyłam przekątne 4 i 6 i z twierdzenia cosinusów zrobiłam trójkąt złożony z połówek przekątnych i dłuższej podstawy powinno wyjść ale mi nie wychodzi co zrobiłam źle ?

prosta: przekątne ; 4 i 2√13.

	2√13
cosinus: −
	13

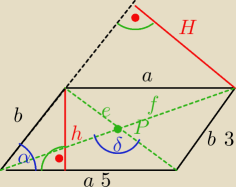Mila: 2a+2b=16 a+b=8 a*2,4=b*4 b=0,6a a+0,6a=8 1,6a=8 a=5 b=0,6*5=3 P_▱=a*h=5*2,4=12 e=4 f=2√13 5²=2²+√13²−2*2*√13 cosδ 25=4+13−4√13*cosδ 8=−4√13*cosδ

	−2
cosδ=
	√13

	−2√13
cosδ=
	13

===============

mysia pysia: dlaczego tam jest ta druga wysokośc nie rozumiem

xyz: Zrobione mysia pysia czego tu nie rozumieć, przecież równoległobok ma dwie wysokości

Mila: Nie zapisałam tam obliczeń do obliczenia długości f, bo wcześniej prosta już obliczyła. Obliczamy cosα z tw. cosinusów w ΔABD

	3
cosα=
	5

	3
cos(180−α)=−
	5

Teraz zastosuj tw. cosinusów do ΔACD.

	3
f2=32+52−2*3*5*(−		)
	5

f²=52 f=2√13 ====

Jack: Milu? https://matematykaszkolna.pl/forum/321178.html Jednak prosiłbym bardzo

Mila: A co tam chciałbyś, abym zrobiła, bo tam już wpisano rozwiązania. Napisz konkretnie.