Udowodnij, że czworokąt jest trapezem
Zaz: Udowodnij, że czworokąt mający kolejne boki o długości 21, 15, 7 i 13 może być trapezem.
Oblicz jego pole.
21 lut 23:02
pigor: ..., pomyśl nad jakimś składnym dowodzikiem, a jest to
trapez o ramionach :
15 (przyległy Δ prostokątny: 15,
12,.9)
i 13 (Δ przyległy prostokątny .13,
12,5)
górnej podstawie 7, dolnej 21 (21= 9+7+5) i wysokości
12;
jego pole więc : P=
12 (21+7)*
12= 6*28= 120+48=
168 . ...

21 lut 23:35
Zaz: Dzięki wielkie!
22 lut 15:09
Wojtek: Mógłbys to dokładniej wytłumaczyć?
16 mar 23:22
a7:
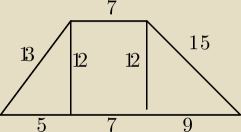
16 mar 23:37
Chila: A jak wpadliście na pomysł, że z tych prostych zrobimy jeden trójkąt a z tych drugich drugi
trójkąt?
16 mar 23:41
a7: ja tylko zrobiłam rysunek, ale jakbym to miała wymyślić to bierzesz dowolny bok jako podstawę
trzeci jako drugą podstawę i sprawdzasz czy ma szansę wyjść trapez, jak weźmiesz 7 i 21 jako
boki a 13 i 15 za podstawy to nijak nie będa one równoległe bo 7 jest za krótki
16 mar 23:45
wredulus_pospolitus:
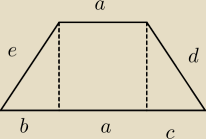
Jeden z dwóch możliwych ogólnych wizualizacji trapezu (jeżeli są różne boki)
Od razu widać, że 'na dole' powinien być największy bok (21).
Reszta to już dopasowywanie (metodą prób i błędów −−− raptem 3 możliwości masz)
Jeżeli nie pasuje ... to trzeba przejść do drugiej 'wizualizacji' trapezu i ponownie próbować
16 mar 23:49
a7:
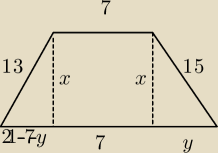
16 mar 23:50
a7: z tw. Pitagorasa
132=x2+(14−y)2
152=x2+y2
y=9 x=12
16 mar 23:56
Wojtek: Dzięki bardzo za pomoc! 😃
17 mar 17:21


 Jeden z dwóch możliwych ogólnych wizualizacji trapezu (jeżeli są różne boki)
Od razu widać, że 'na dole' powinien być największy bok (21).
Reszta to już dopasowywanie (metodą prób i błędów −−− raptem 3 możliwości masz)
Jeżeli nie pasuje ... to trzeba przejść do drugiej 'wizualizacji' trapezu i ponownie próbować
Jeden z dwóch możliwych ogólnych wizualizacji trapezu (jeżeli są różne boki)
Od razu widać, że 'na dole' powinien być największy bok (21).
Reszta to już dopasowywanie (metodą prób i błędów −−− raptem 3 możliwości masz)
Jeżeli nie pasuje ... to trzeba przejść do drugiej 'wizualizacji' trapezu i ponownie próbować
