nierówność bogusia: rozwiąż nierówność √3 f(x) < − −−−−−−− 2

bogusia: Narysuj wykres funkcji f(x) = sin x, pi gdzie x ∊ < − −−−− , 2pi , a następnie : podaj miejsce zerowe funkcji f; 2

bogusia: zapomniałam nawiasu >

bogusia: Narysuj wykres funkcji f(x) = sin x, pi gdzie x ∊ < − −−−− > , 2pi , a następnie : podaj miejsce zerowe funkcji f; 2

bogusia: ?

bogusia: Narysuj wykres funkcji f(x) = sin x, π gdzie x ∊ < − −−−− > , 2π , a następnie : podaj miejsce zerowe funkcji f; 2

bogusia:

bogusia: pomożecie

Eta: zobacz tu; 426

bogusia: rozwiąż nierówność √3 f(x) < − −−−−−−− 2

Nikka: dla tej samej funkcji?

bogusia: to jest przykład b: tamten był przykład a:

bogusia: tak do tej samej

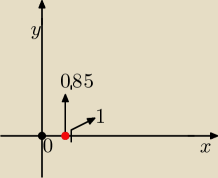
Dawiddic: Oszacuj miej więcej ile to √3(od razu mowie ze √3≈1,7 i masz: ^1.7₂=0,85 A więc f_(x)≈0,85 czyli na osi x będzie kropka w punkcie 0,85 I to przybliżone rozwiązanie

bogusia: Tu byó trzeba rozwiązać nierówność √3 f(x) < − −−−−−−− 2

bogusia: było

bogusia: pomożecie

bogusia: rozwiąż nierówność √3 f(x) < − −−−−−−− 2

AROB: Pomogę Ci Bogusiu

AROB:

	π
Zad. 1. Wykres funkcji f(x) = sinx dla x∊ < −		, 2π >
	2

Miejsca zerowe: x ∊ { 0, π, 2π } Zaraz spróbuję zrobić wykres do zad 2.

AROB:

	√3
Zad. 2. Rozumiem, że nierówność f(x) < −		ma być rozwiązana także w przedziale
	2

	π
< −		, 2π>.
	2

	√3
Przerywana linia przechodzi przez punkt −		≈ − 0,85
	2

	√3
Wyznaczamy najpierw rozwiązania równania sinx = −		w żądanym przedziale.
	2

	π		4
Są nimi: x1 = π +		=		π
	3		3

	π		5
x2 = 2π −		=		π
	3		3

	π
x3 = −
	3

Rozwiązaniem nierówności są przedziały oznaczone na rysunku kolorem czerwonym.

	π		π		4		5
Czyli: x∊ < −		, −		) ∪ (		π,		π)
	2		3		3		3

bogusia: Jejku jak pięknie narysowane i wytłumaczone Wielkie dzięki