Pewna nierówność...
Phoebe Campbell:
Dlaczego dla k2 − 2k + 3 > 0 k∊R?
20 lut 21:36
jakubs: A naszkicuj sobie tę parabolę i zobaczysz

20 lut 21:37
panpawel: a no dlatego

k
2 − 2k + 3=(k−1)
2+2
20 lut 21:37
Qulka:
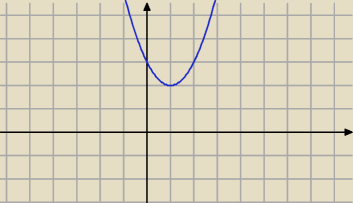
20 lut 21:44
Phoebe Campbell: jakubs − ogólnie mówiąc szkicowanie/rysowanie to nie jest moja mocna strona...
no i coś tam naszkicować umiem tylko kiedy mam pierwiastki..
można bez nich też cokolwiek rysować?
panpawel − nie wpadłem na to żeby tak to zapisać, dzięki

20 lut 21:44
jakubs: To poćwicz, wystarczyło mieć współrzędne wierzchołka i współczynnik przy k
2 czyli 1

20 lut 21:48
pigor: ..., bo istotne jest to , że tu
... >0 rzędne (y−eki) punktów
(k,y) paraboli danej wzorem y=k
2−2k+3 dla każdej wartości
odciętej k ze zbioru R, czyli dla "wszystkich" k∊R są dodatnie tzn.
y= k
2−2k+3 >0, graficznie
cała parabola leży sobie nad osią
OX (nie przecina osi tej OX) o czym "mówi nam]] znak ujemny
"delty" trójmianu zmiennej k :y= k
2−2k+3, istotnie, tu Δ
k=(−2)
2−4*1*3=
4−12=−8< 0 i to tyle

20 lut 21:50
20 lut 21:50
Phoebe Campbell: pigor − nawet nie wiedziałem, że ujemna delta świadczy o nieprzecinaniu się paraboli z OX...
Muszę jeszcze sporo nad tym wszystkim posiedzieć

20 lut 21:52
Metis: Mówiąc dokładniej to nie do konca ujemna delta o tym świadczy a fakt, że dana funkcja po prostu
nie ma miejsc zerowych...
20 lut 21:58
Phoebe Campbell:
To już sobie przed chwilą "wydedukowałem" zastanawiając się nad tym co zmienia ujemna delta

20 lut 22:01

 k2 − 2k + 3=(k−1)2+2
k2 − 2k + 3=(k−1)2+2





