trygonometria trygonometria: Witam, nie rozumiem jak zostały tu określone przedziały monotoniczności Dlaczego malejąca w przedziałach (4kπ,2π+4kπ) Pomoże ktoś to zrozumieć? https://matematykaszkolna.pl/strona/1536.html

Qulka: bo jak patrzysz w kierunku osi x i idziesz po funkcji to schodzisz z górki (malejąca) czy wchodzisz pod górkę (rosnąca)

Metis: Zajrzyj do komentarzy Jakub już wyjaśniał tą kwestię. https://matematykaszkolna.pl/forum/forum.py?komentarzdo=1536

Metis: *tę

trygonometria: w końcu się udało zrozumieć a podacie jakieś wskazówki do narysowania wykresu : y=cos ^x+π₂ jak tutaj będzie z przesuwaniem ? cosx −> cos^x₂ −− wektor[−π,0] −>y ?

trygonometria: wiem ,że są przykłady, ale pierw chcę spróbować sam, to więcej i na dłużej zapamiętam

trygonometria:

trygonometria: ma ktos pomysl jak to narysowac?: p

Gray: Dobrze napisałeś o 20:49.

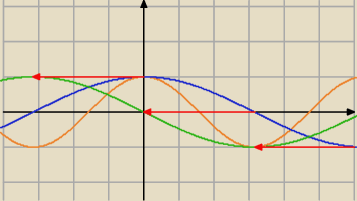
Qulka: żółta cosx niebieska cos(x/2) zielona cos((x+π)/2)

trygonometria: pięknie dziękuję

trygonometria: jeszcze mam takie pytanko dlaczego miejsce zerowe sinusa określamy jako x=kπ , a cosinusa jako x=^π₂+2kπ ?

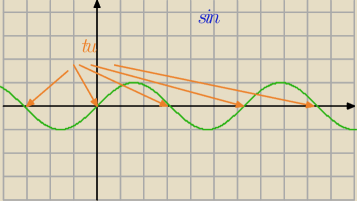
Qulka: tam czyli w 0 potem π dalej i znów π dalej i znów π dalej i znów π dalej i znów π dalej i znów π dalej w skrócie co kπ

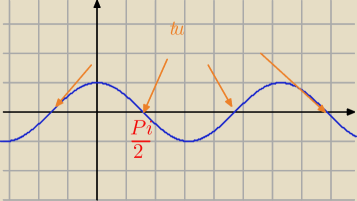
Qulka: a cosx to π/2 i też co kπ

trygonometria: ok dzięki a mam teraz takie narysować i odczytac f(x)>0 : f(x)=sin(2x+π) kolejno : sinx−>sin2x−wektor[−π,0]−> f(x) i f(x)>0 wyszło mi w przedziałach (kπ,^π₂+kπ) nie wiem czy dobrze, pomożesz w sprawdzeniu ?

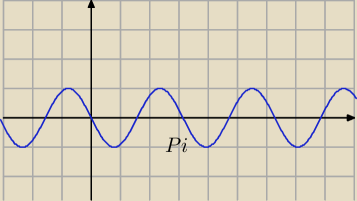
Qulka: x∊ (π/2+kπ;π+kπ)

trygonometria: ciekawe gdzie mam błąd:( bo mi wyszedł ten wykres dokładnie odwrotnie tak jakby symetrycznie OX

trygonometria: jeśli ten wykres przesuniemy o −π to chyba będzie wyglądał tak samo? https://matematykaszkolna.pl/strona/1535.html

trygonometria: ehhhh... nie wyciągnąłem przed nawias 2 i dlatego mi tak wyszło

trygonometria: i czy podczas rysowania wykresów sin(2x+..) zawsze muszę zapisywać jako sin2(^x₂+..) jak jest sinus ? a jak jest cosinus to bez wyciągania 2 przed nawias?

trygonometria: dobra,to też mi się udało rozwikłać. a taki wykres: f(x)=tg(x−^π₄) f(x)>0 wyszło mi przedział (^π₄+kπ,⁵₄π+kπ)

trygonometria: w odp pisze ,że do 3/4 π+kπ

trygonometria: pomoze ktos ?

Qulka: bo wektorem jest π/2 bo podlega temu działaniu co x więc jak masz 2x to przesuwasz o π/2 bo będzie 2(x−π/2) = 2x − π

Qulka: w cosinusie miałeś π w mianowniku czyli było dzielone przez dwa tak jak x i dlatego było o π

Qulka: tu masz fajną sprawdzajkę http://www.wolframalpha.com/input/?i=tg%28x%E2%88%92%CF%80%2F4%29+%3E0

trygonometria: ok bardzo dziękuję, przyda się

trygonometria: ok reszte mam dobrze, zostało tylko to z tym tangensem

trygonometria: będę siedział dopóki nie zrozumiem ,bo założyłem że dziś zrobię 8 zadań i muszę je zrobić

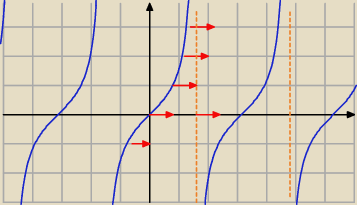
Qulka: asymptota się przesuwa z π/2 do π/2 +π/4 czyli 3π/4

trygonometria: no tak, ale chyba tangens przecina oś ox w ^π₄ oraz ⁵₄π itd jeśli się tak to poprzesuwało

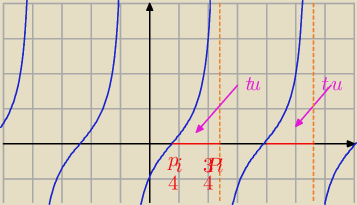
Qulka: no więc po przesunięciu x∊(π/4 +kπ ; 3π/4+kπ) pytałeś czemu do 3π/4+kπ bo się przesunęła asymptota a za asymptotą już jest ujemne więc nie należy

Qulka:

trygonometria: aaaaaaaaaaaa ale jetem tępy dobra, już za długo siedzę. to przez te zaległości teraz dopiero zaczynam się "praktycznie" uczyć tej trygonometrii jeszcze czeka mnie dokończenie trygonometrii, ciągi , rachunek różniczkowy i powtórzenie prawdopodobieństwa ciekwe czy zdążę w każdym bądź razie wielkie dzięki za pomoc i poświęcony mi czas na te zadanka z trygonometrii