proszę o rozwiązanie Michał: Punkty B = (6,2) i C(−1, 3) są końcami przeciwprostokątnej trójkąta ABC , przy czym A jest punktem prostej 2x − y = 0 Wyznacz współrzędne punktu A I AB I ⊥ I ACI i A ( x , 2x) bo ∊ do prostej y = 2x

	1		20
obliczyłem prostą przechodzącą przez B i C y = −		x +
	7		7

dalej nie mam pomysłu

Eve: A(x,y) może wektorowo będzie łatwiej

Eve:

Michał:

	5		5
już obliczyłem znalazłem połowę odcinka BC ⇒ D = (		,		}
	2		2

a następnie prostą prostopadłą do CB i przechodzącą przez punkt D czyli y = 7x −15 wspólrzędną punktu A obliczyłem rozwiązując układ równań y = 7x −15 i y = 2x A =( 3, 6) tylko w wyniku jest jeszcz jeden punkt A = ( 0, 0) inie wiem jak to obliczyć

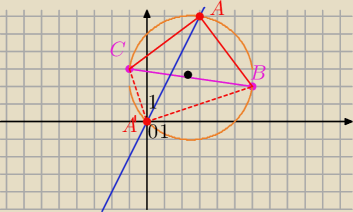
Mila: B = (6,2) i C(−1, 3) BC− przeciwprostokątna

	6−1		2+3		5		5
S=(		,		)=(		,		) środek BC, środek okręgu opisanego na ΔBCA.
	2		2		2		2

SB²=(6−2.5)²+(2−2.5)² SB²=r²=3.5²+0.5²=12.25+0.25=12.5 (x−2.5)²+(y−2.5)²=12.5 podataw y=2x (x−2.5)²+(2x−2.5)²=12.5 x=0, y=0⇔A=(0,0) lub x=3, y=6⇔A=(3,6) ∡CAB=90^o jako wpisany w okrąg, oparty na średnicy.

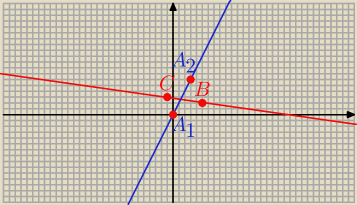
Janek191: A ( x , 2 x) więc → AC = [ − 1 − x; 3 − 2 x ] → AB = [ 6 − x ; 2 − 2 x] Te dwa wektory są prostopadłe, więc ( − 1 − x)*( 6 − x) + ( 3 − 2 x)*( 2 − 2 x) = 0 − 6 + x − 6 x + x² + 6 − 6 x − 4 x + 4 x² = 0 5 x² − 15 x = 0 5 x*( x − 3) = 0 x = 0 lub x = 3 więc y = 0 lub y = 6 A = ( 0, 0) lub A = ( 3 ; 6) ====================

Eta: I znów gotowiec ( wkurzające to ! wystarczyło dać wskazówkę : wykorzystaj prostopadłość wektorów!

Eve: ja juz się nie wkurza, się przyzwyczaiłam

Michał: podziękowania dla Mili i Janek191

Michał: jeszcze mam jedno zadanie Prosta prostopadła do przeciwprostokątnej BC trójkąta ABC przecina ją w punkcie L a przyprostokątną AB w punkcie K Udowodnij że I ∠ CAL I = I ∠ CKL I

Michał: wykorzystałemże na czworokącie AKLC można opisać okrąg i z tw że iloczyn długości jego przekątnychjest równy sumie iloczynów długości boków przeciwległych czworokąt AKLC I CK I = IxI I AL I = Iy I IxI*IyI = ab +cd AK = a KL = d LC = b AC = c a następnie chcę skorzystać z tw cos czy dobra jest ta myśl

Eta:

Michał: ponadto wiem że ∠CKL = ∠CAL − jako kąty wpisane oparte natym samym łuku

Eta: I na tym koniec dowodu

gargamel: dla Etusi z okazji walentynek

Eta: Dziękuję

Michał: czyli wystarczy taki wniosek

Eta: Tak ( tylko ładnie napisać stosowny komentarz

Michał: dziękuję

Metis: Eta, Milu sprawdzicie rozwiązanie kolegi w 280004 , mam wątpliwości do co przeprowadzonego dowodu.

panpawel: jakie wątpliwości?

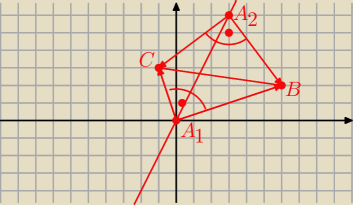
Gustlik: Punkty B = (6,2) i C(−1, 3) są końcami przeciwprostokątnej trójkąta ABC , przy czym A jest punktem prostej 2x − y = 0 Wyznacz współrzędne punktu A 2x − y = 0 ⇔ y=2x ⇔ A=(x, 2x) B = (6,2) C(−1, 3) Z wektorów: AB^→=[6−x, 2−2x] AC^→=[−1−x, 3−2x] Wektory są prostopadłe ⇔ iloczyn skalarny AB^→*AC^→= 0 Iloczyn skalarny się bardzo prosto liczy: https://matematykaszkolna.pl/strona/1629.html − mnożymy "kolumnowo" czyli współrzedną x−owa jednego wektora przez x−ową drugiego wektora i tak samo y−owa przez y−ową i dodajemy. AB^→*AC^→=(6−x)(−1−x)+(2−2x)(3−2x)=−6−6x+x+x²+6−4x−6x+4x²=5x²−15x 5x²−15x=0 /:5 x²−3x=0 x(x−3)=0 x=0 v x=3 y=2x y=o v y=6 Są 2 takie punkty: A₁=(0, 0) i A₂=(3, 6)

Michał: dziękuję bardzo