rownanko do sprawdzenia.
funkcja: witajcie,
proszę o rozwiązanie: |x−1|+|x+3|=4
próbuję to zrobić na przedziałach i wychodzi mi inaczej niż w odpowiedzi:
1) x∊(−∞,−3>
−x+1+x+3=4
4=4
wszystkie liczby w tym przedziale
2) x∊(−3,1)
−x+1−x−3=4
x=−3
3) x∊<1,∞)
x−1+x+3=4
x=1
Odp: x∊(−∞,−3> u {1}
w książce jest: x ∊ <−3, 1>
15 lut 16:07
funkcja: halo?

15 lut 16:19
Metis: Już rozwiązuję.
15 lut 16:21
funkcja: ok dziękuję, czekam.
15 lut 16:22
PW: 279886 − spróbuj pomyśleć tak jak tu.
15 lut 16:23
Draghan:
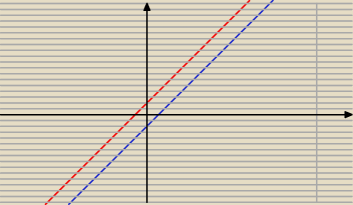
Na wykresie (coś mi niedokładnie wyszedł, ale to nic):
x+3,
x−1. Obydwie funkcje są rosnące.
Dla x ∊ (−oo; −3) masz równanie:
−(x−1)
− (x+3) = 4
Dla x ∊ <−3; 1) masz:
−(x−1) + (x+3) = 4
A dla reszty zakresu (x−1) + (x+3) = 4
15 lut 16:24
funkcja: czyli nie mogę wziąć pierwszego przedziału jako (−∞,−3>? dlaczego nie mogę wziąć domkniętego?
nie bardzo rozumiem.
15 lut 16:28
Metis: Rozwiązujesz w przedziałach:
1) x∊(−∞, −3)
2) x∊[−3, 1)
3) x∊[1, +∞)
1) Dla x∊(−∞, −3) równanie |x−1|+|x+3|=4 przyjmuje postać:
−(x−1)−(x+3)=4
−x+1−x−3−4=0
−2x −6=0
−2x=6 /:(−2)
x=−3
Nie zawiera się w przedziale.
2) Dla x∊[−3, 1) równanie |x−1|+|x+3|=4 przyjmuje postać:
−(x−1)+(x+3)=4
−x+1+x+3−4=0
0=0
Nieskończenie wiele rozwiązań zatem x∊[−3, 1)
3) Dla x∊[1, +∞) równanie |x−1|+|x+3|=4 przyjmuje postać:
(x−1)+(x+3)=4
x−1+x+3−4=0
2x=2
x=1
Łaczymy odpowiedzi uzyskane wcześniej, czyli:
x∊[−3, 1]
15 lut 16:30
Draghan: Możesz wziąć jako domknięty, to nie ma znaczenia, bo są różne definicje wartości bezwzględnej.
I tak i tak jest poprawnie.
Ale spójrz na same równania − porównaj Twoje z moimi.

15 lut 16:31
funkcja: analizowałem, i wychodzi, że to ma jednak znaczenie.
spójrz, proszę:
x∊(−∞,−3>
|x−1|+|x+3|=4
−(x−1)+(x+3)=4
−x+1+x+3=4
4=4
lub
x ∊ (−oo; −3)
−(x−1) − (x+3) = 4
−x+1−x−3=4
−2x=6
x=−3
więc dlaczego jak domykam to wychodzi 4=4? wtedy "prawdziwy" jest cały przedział, co już daje
złą odpowiedź.
15 lut 16:34
funkcja: tak samo Metis − również domknął z drugiej strony. już nie łapię − jak to jest?

15 lut 16:35
Draghan: Źle rozpisujesz równanie. Dla tego przedziału OBA "MODUŁY" muszą być ujemne.

15 lut 16:35
funkcja: −3+3=0 więc znaku chyba nie zmieniam?
15 lut 16:37
Draghan: Musisz zmienić znak, bo rozpatrujesz iksy MNIEJSZE (lub równe) wartości zerującej "moduł".
A co do tego, gdzie domykać, a gdzie otwierać:
| | ⎧ | x dla x ≥ 0 | |
| |x| = | ⎩ | −x dla x < 0 |
|
Jest tożsamościowe z:
| | ⎧ | x dla x > 0 | |
| |x| = | ⎩ | −x dla x ≤ 0 |
|
Bo ważne jest tylko, żebyś uwzględnił w równaniu przypadek z zerem, nieważne, czy będzie on ≥,
czy ≤, bo −0 = 0.
Spróbuj sobie zrobić jakiś prosty przykład dwoma sposobami − raz z domykaniem z jednej, a raz z
drugiej strony. Musi wyjść to samo.

15 lut 16:41
5-latek: Moze inaczej
Do tego zeby sprawdzic czy to co jest w module ujemne czy dodatnie nie bierzesz liczb
skrajnych
np dla xe(−oo −3) wez sobie np x=−100 x=−4
to samo jesli masz xe(−oo −3> tak samo nie bierzesz skrajnych
15 lut 16:41
funkcja: czyli nie zmieniam znaku gdy dla danego modułu wszystkie iksy robią z zawartości modułu liczbę
nieujemną, zgadza się?
trochę niejasno napisałem

15 lut 16:43
PW: Panowie, po co tyle trudu? Jest to typowe zadanie "na interpretację geometryczną" − ponownie
zachęcam:
279886.
15 lut 16:43
funkcja: PW, patrzyłem, ale mnie interesuje taka metoda o jaką tutaj toczymy spór

15 lut 16:45
Draghan: ...a najłatwiej zapamiętać to, co
5−latek napisał.

A
PW również radziłbym posłuchać, bo dobrze radzi.

Witam i pozdrawiam.

Patrzyłem na te książki, do których mi link wysłałeś,
5−latek.

Może sobie coś zamówię.

Posiadasz może któreś z nich u siebie? W sensie, że mogłeś je sobie
przejrzeć?
15 lut 16:46
funkcja: no to tak jak mówię: WSZYSTKIE WARTOŚCI IKSA z danego przedziału muszą dać w module liczbę
nieujemną by mozna było zostawić znaki bez zmiany, tak?
15 lut 16:47
Draghan: No właśnie.

Słowo−klucz: nieujemną.

15 lut 16:48
funkcja: to chyba już jasne, dziękuję
15 lut 16:49
5-latek: Czesc
Draghan 
Posiadam wszystkie te ksiazki ktore tytuly CI napisalem
15 lut 16:55
15 lut 16:59
5-latek: Tyle starczy (bo co za duzo to niezdrowo tak mowia

15 lut 17:00
Draghan: A jakie zagadnienia są poruszane w "Algebra zbiór zadań z matematyki elementarnej" A.
Ehrenfeucht, O. Stande? Tak z grubsza.

Chciałem sobie podejrzeć gdzieś on−line, ale nie
mogłem znaleźć.
15 lut 17:00
Dziadek Mróz:
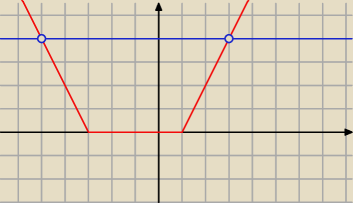
|x − 1| + |x + 3| = 4
| | ⎧ | −x dla x < 0 | |
| |x| = | ⎩ | x dla x ≥ 0 |
|
x < 0:
−(x − 1) + (−(x + 3)) = 4
−x + 1 − x − 3 = 4
−2x = 6
x = −3
x ≥ 0
x − 1 + x + 3 = 4
2x = 2
x = 1
x ∊ {−3, 1}
15 lut 17:07
15 lut 17:07
Dziadek Mróz:
Rysunek jest zły
15 lut 17:07
Dziadek Mróz:
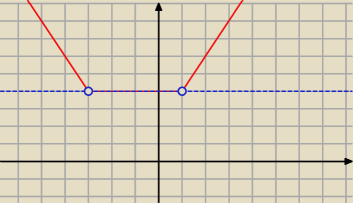
15 lut 17:08
Metis: Poszukaj wersji z 2000 roku

15 lut 17:09
5-latek: Juz Ci piszse z gubsza
1. Elementy logiki i nauki o zbiorach
2. Relacja ,dzialania grupy cialo
3. Cwiczenia rachunkowe i wlasnosci liczb
4. Ogolne wlasnosci funkcji
5. Funkcja liniowa
6. Funkcja drugiego stopnia
Funkcje wymierneI . Wielomiany
8. Funkcje wymierne II.
9. Funkcja potegpowa
10 Funkcja wykladnicza i logarytmiczna
11. Funkcje trygonometryczne.
12. Ciagi
13. Granica , ciaglosc i pochodna funkcji
14. Dalsze wiadomosci pochodnych ,calka
15. Liczby i zmienne zespolone (malo zadan
15 lut 17:09
funkcja:
|x|+|x−3|=3
1) x∊(−oo,0)
−x−x+3=3
−2x=0
2)x∊<0,3)
x−x+3=3
0=0
cały przedział
3)x∊<3,+00)
x+x−3=3
2x=6
x=3
odp: x∊<0,3>
teraz dobrze?

15 lut 17:13
5-latek: Ja mam ja z 1973r ta algebre
15 lut 17:13
Metis: A mi chodzi akurat o Gdowskiego / Plucińskiego .

15 lut 17:15
5-latek: Czesc
Metis 
ja wiem ze Tobie chodzilo o ta ksiazke
15 lut 17:18
Metis: 
15 lut 17:20
5-latek: funkcja
nalezy napisac tak
W 1 przedziale nie ma rozwiazan bo x=0 nie nalezy do tego przedzialu
W2 drugim przedziale mamy rownanie tozsamosciowe weic caly tem przedzial xe(<0.3) jest
rozwiqazaniem tego rownania
w 3 przedziale x=3 jest rozwiazniem tego rownania bo x=3 nalezy do tego przedzialu
A wiec rozwiazniem tego rownania jest xe(<0,3>
15 lut 17:22
5-latek: oczywiscie na koncu ma byc x∊<0,3>
15 lut 17:24
Draghan: Metis, czemu z 2000?

Aż tak poprawiona wersja?

15 lut 17:27
Metis: Przepiszę Ci wstęp z przedmowy do wydania XVI − 1999r

15 lut 17:29
funkcja: czyli dobrze zrobiłem

ok dzięki wszystkim, już łapię

15 lut 17:33
Metis: Od pierwszego wydania niniejszej książki minęło 28 lat. Korzystało z niej tysiące nauczycieli i
setki tysięcy uczniów. Z pełną satysfakcją przekazujemy do rąk Czytelnika kolejne jej wydanie.
Mamy nadzieje ze jak dotąd skorzystają z niej uczniowie szkół średnich maturzyści i zdający
egzaminy wstępne do różnego rodzaju szkol wyższych od uniwersytetów po szkoły zawodowe.
Załączone na końcu książki zestawy zadań z egzaminów wstępnych( zawsze z ost. 4 lat) pozwolą
na wyrobienie sobie przez Czytelników poglądów na temat relacji między zadaniami zawartymi w
książce a zadaniach na egzaminach wstępnych.
Warszawa 1999
Edmund Pluciński
Bogusław Gdowski
15 lut 17:36
Draghan: Hmm.

Znalazłem w pdf wersję z '73 bodajże. Po wstępnym przejrzeniu uznałem, że jest świetna.
Myślisz, że nie obniżyli poziomu w wydaniu z 2000r.?

15 lut 17:39
5-latek: Pewnie ze nie

15 lut 17:41
Metis: Nie

To dobry zbiór. Zadania są nietknięte, odswiezyli tylko okładkę i dodali dodatkowe zestawy
zadań na końcu.
15 lut 17:41
Draghan: 
No to leci do mnie!

15 lut 17:44

 Na wykresie (coś mi niedokładnie wyszedł, ale to nic):
x+3, x−1. Obydwie funkcje są rosnące.
Dla x ∊ (−oo; −3) masz równanie:
−(x−1) − (x+3) = 4
Dla x ∊ <−3; 1) masz:
−(x−1) + (x+3) = 4
A dla reszty zakresu (x−1) + (x+3) = 4
Na wykresie (coś mi niedokładnie wyszedł, ale to nic):
x+3, x−1. Obydwie funkcje są rosnące.
Dla x ∊ (−oo; −3) masz równanie:
−(x−1) − (x+3) = 4
Dla x ∊ <−3; 1) masz:
−(x−1) + (x+3) = 4
A dla reszty zakresu (x−1) + (x+3) = 4






 A PW również radziłbym posłuchać, bo dobrze radzi.
A PW również radziłbym posłuchać, bo dobrze radzi.  Witam i pozdrawiam.
Witam i pozdrawiam.  Patrzyłem na te książki, do których mi link wysłałeś, 5−latek.
Patrzyłem na te książki, do których mi link wysłałeś, 5−latek.  Może sobie coś zamówię.
Może sobie coś zamówię.  Posiadasz może któreś z nich u siebie? W sensie, że mogłeś je sobie
przejrzeć?
Posiadasz może któreś z nich u siebie? W sensie, że mogłeś je sobie
przejrzeć?
 Słowo−klucz: nieujemną.
Słowo−klucz: nieujemną. 
 Posiadam wszystkie te ksiazki ktore tytuly CI napisalem
Posiadam wszystkie te ksiazki ktore tytuly CI napisalem


 Chciałem sobie podejrzeć gdzieś on−line, ale nie
mogłem znaleźć.
Chciałem sobie podejrzeć gdzieś on−line, ale nie
mogłem znaleźć.
 |x − 1| + |x + 3| = 4
|x − 1| + |x + 3| = 4
 zamawiam! Dzięki
zamawiam! Dzięki






 ja wiem ze Tobie chodzilo o ta ksiazke
ja wiem ze Tobie chodzilo o ta ksiazke

 Aż tak poprawiona wersja?
Aż tak poprawiona wersja? 

 ok dzięki wszystkim, już łapię
ok dzięki wszystkim, już łapię
 Znalazłem w pdf wersję z '73 bodajże. Po wstępnym przejrzeniu uznałem, że jest świetna.
Myślisz, że nie obniżyli poziomu w wydaniu z 2000r.?
Znalazłem w pdf wersję z '73 bodajże. Po wstępnym przejrzeniu uznałem, że jest świetna.
Myślisz, że nie obniżyli poziomu w wydaniu z 2000r.? 

 To dobry zbiór. Zadania są nietknięte, odswiezyli tylko okładkę i dodali dodatkowe zestawy
zadań na końcu.
To dobry zbiór. Zadania są nietknięte, odswiezyli tylko okładkę i dodali dodatkowe zestawy
zadań na końcu.
 No to leci do mnie!
No to leci do mnie! 