maturzyści... trójkąt: maturzyści.. czy są tu jacyś maturzyści przygotowujący się ze zbioru kiełbasy? jak wam idzie planimetria z tego zbioru? u mnie to kompletna katastrofa, nie jestem w stanie zrobić większości zadań... te zadania są takie trudne czy po prostu mam takie braki z planimetrii? nie mogę przebrnąć przez ten dział, idzie to mozolnie i muszę 80% zadań sprawdzać w internecie, bo nie jestem w stanie nawet ich ruszyć..

ajć:

Qulka: wszystko jest trudne nim stanie się proste trzeba po prostu podchodzić z nastawieniem, że to fajne i ciekawe , a nie że obowiązek i konieczność

trójkąt: staram się, ale jak od tygodnia robię te zadania a nadal nic mi nie wychodzi, to trochę to zniechęca szczególnie że czasu mało a ja potrzebuję około 90% z rozszerzenia. żaden inny dział nie sprawia mi takich trudności(nie licząc stereometrii, ale to dopiero przede mną w szkole )

Draghan: Łapaj kilka ogólnych wskazówek. https://matematykaszkolna.pl/forum/246565.html

Qulka: stereometrię i tak zawsze rozkładasz na płaskie, więc bez planimetrii nic nie zrobisz

trójkąt: o dzięki @Qulka, ale stereometrię często da się rozwalić z twierdzenia Pitagorasa idę spać, rano wstaję − przeczytam wskazówki i kontynuuję zadanka. dobrej nocy.

trójkąt: edit: nie myślnik a przecinek... o czym ja myślał∊m..

panpawel: Ja jestem tegorocznym maturzystą i mam zupełnie odwrotnie niż Ty

trójkąt: w jakim sensie? że planimetria z kiełbasy jest dla Ciebie prościzną?

Krystii: Znam ten ból. Jestem tegorocznym maturzystą i planimetria to moja pięta Achillesa

trójkąt: @Draghan, jedno z danych twierdzeń na tamtej stronie: "w trójkącie prostokątnym wysokość poprowadzona z wierzchołka kąta prostego dzieli ten trójkąt na trzy podobne do siebie", czy takie wykazanie jest dobre? 1) oznaczam kąt 90^o, kąt α oraz kąt 90−α 2) prowadzę wysokość i zaznaczam dwa kąty proste u podstawy wysokości oraz zauważam, że dzieli ona trójkąty na trzy podobne ze względu na kąt−kąt−kąt będzie ok? narysowałbym ale nie umiem @Krystii przynajmniej nie jestem sam

Kacper: Nie martwcie się, planimetria sprawia też kłopoty nauczycielom Tutaj obowiązuje zasada, że trzeba rozwiązać dużą liczbę zadań, żeby zauważać pewne związki Potem nagle dostajesz nowe zadanie i żadne z wcześniejszych rozwiązań nie pasuje i myślisz od nowa I za to kocham planimetrię

kyrtap:

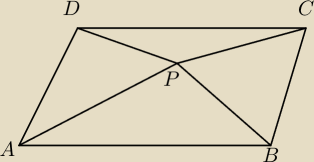
trójkąt: a ja nienawidzę! skorzystam z okazji: punkt P należy do wnętrza równoległoboku ABCD. wykaż, że suma pól trojkątów ABP i CDP jest równa połowie pola równoległoboku ABCD. zauwazylem, nie wiem czy slusznie, ze trójkąty te maja ten sam kąt przy wierzchołku P oraz tę samą postawę, i dalej nic nie mogę ruszyć tego zadanka. jakaś wskazówka?

Krystii: Napisz sobie wzór na pole trójkątów i równoległoboku. oznacz wysokości h₁ i h₂ gdzie h₁+h₂=h zauważ że skoro jest to równoległobok to |AB|=|CD|

trójkąt: nie zauważyłem h₁ + h₂=h teraz już rozwiązałem bez problemu.

panpawel: @trójkąt: ze trójkąty te maja ten sam kąt przy wierzchołku P które kąty?

trójkąt: no tak.. od razu się rzuciłem, że to kąty wierzchołkowe ale w tym zadaniu i tak nie było to na szczęście istotne.

Kuba: http://pl.static.z-dn.net/files/d32/271376be806342e880b0599909367be1.jpg Pomoze ktos