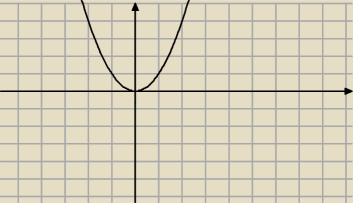
obrazy i przeciwobrazy 5-latek: Wroce do obrazow i przeciwobrazow funkcji Dla f(x)=x² znajdz obrazy f(R)=R f(<0,oo))=<0,oo) Dla tej samej funkcji znajdz przeciwobrazy zbiorow : {0} to f⁻1({0})=0 {1} to f⁻1({1})={−1,1} <0,1> to f⁻1(<0,1>)=<0,1> <−1,1> to f⁻1(<−1,1>)=<0,1>

Eve: ok dzień dobry 5−latku

5-latek: Dzien dobryEve Pozdrawiam To fajnie

Gray: Cześć: dwie usterki: f⁻¹([0,1])=[−1,1] f⁻¹{[−1,1])=[−1,1]

5-latek: Czesc Gray Co do pierwszsego co napisales to tez sie zastanawialem nad tym czy dobrze napisalem bo funkcja osiaga wartosc y=− dla x=−1 natomiast co do drugiego zapisu mam pewne wattpliwosci gdyz funkcja ta nie osiaga wartosci y=−1

5-latek: Mialobyc y=1 dla x=−1

Gray: Nie rozumiem − skąd Twoje wątpliwości? Jest tak f⁻¹([−1,1])=... funkcja osiąga jedynie wartości nieujemne ... = f⁻¹([0,1])=[−1,1]

5-latek: Pierszy jest OK natomiast ten zapis f⁻¹([−1,1] =[−1,1] tak zapisales TY Wlasnie co do tego mam watpliwosc Nie wiem czy uzasadniona bo tak na chlopski rozum (musimy znalezc takie x_sy dla ktorych ta funkcja osiaga takie wartosci . Ale ta funkcja nie osiaga wartosci ujemnych . Wiec przeciwobrazem nie moze byc ten przedzial ktory zapisales . tak mysle

5-latek: Przepraszam ze tak to draze

Gray: Jest OK. Rozpiszę to z definicji: f⁻¹([−1,1])={x∊R: f(x)∊[−1,1]}={x∊R: −1≤x²≤1}={x∊R: −1≤x²⋀ x²≤1}= {x∊R: −1≤x²}∩{x∊R: x²≤1}=R∩{x∊R: x²≤1}={x∊R: x²≤1}={x∊R: |x|≤1}=[−1,1]. Nie chce być inaczej...

Eve: przepraszam Gray szukamy błędu, pomóż https://matematykaszkolna.pl/forum/279202.html

5-latek: Dobrze . rano przepiszse to do zeszytu i przeanalizuje dzisiaj juz nie