nierownosc z wartoscia bezwzgledna Rose: jak rozwiazac rownanie x²−|x−3|≥2x+3 prosze tez o tlumaczenie

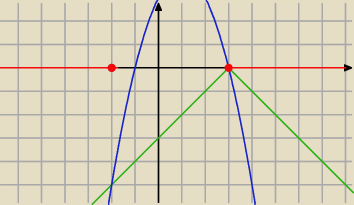
Marcin: −|x−3|≥−x²+2x+3

Rose: a tak pisemnie bez rysowania?

Marcin: Dla x≥3 i dla x<3 osobno

Rose: dzieki pomoglo

Rose: ale nwm czemu w https://matematykaszkolna.pl/forum/279019.html to nie pomoglo ta metoda mnie pierwszy raz zawiodla

Marcin: To nie metoda Cię zawiodła, tylko raczej popełniłeś błąd w obliczeniach

Rose: byc moze ej bo mam teraz Δ=9 x≥3 i Δ=25 x<3 x=0 x=−2 x=3 x=3 jak mam wykresy(falki czy tam wezyki) do tego zrobic a>0 w obu rownaniach n bo w pierwszym 0 nie nalezy do D a w drugim −2 nie nalezy do D niby liczby te powiiny byc dobre bo w jakis tam sposob beda w tym przedziale koncowym (czytam z twojego wykresu od −∞ do −2 oraz od 3 do +∞) ale jak mam to teraz pociagnac?

Rose: jestes tam jeszcze?

Qulka: zrobić wężyki do każdego oddzielnie i dopiero potem dołożyć do wyników dziedzinę

Rose: aaa takie to buty

Marcin: Masz nierówność, a nie równanie. Więc jakie masz przedziały dla x≥3, a jakie dla x<3? Uwzględniaj dziedzinę

Rose: bede pamietac

Rose: juz mi wyszlo thx

Metis: Po co komu wykresy ? x²−|x−3|≥2x+3 1) x∊(−∞,3) Nierówność przyjmie postać: x²−(−x+3)≥2x+3 x²+x−3≥2x+3 // porządkujemy x²+x−2x−3−3≥0 x²−x−6≥0 x∊(−∞, −2] U [3,+∞) Konfrontujemy z założeniem: Zatem x∊(−∞, −2] 2) x∊[3,+∞) Nierówność przyjmie postać: x²−(x−3)≥2x+3 x² −x+3≥2x+3 //porządkujemy x² −x−2x+3−3≥0 x²−3x≥0 x∊(−∞,0] U [3,+∞) Konfrontujemy z założeniem: Zatem x∊[3,+∞) Ostateczna odpowiedź: x∊(−∞, −2] U [3,+∞)...