Pytanie m.: Gdy z rozwiązywanej nierówności wyjdzie mi np −3 ≤ −3 to jest nieskonczenie wiele rozwiązan?

Matematyk: Jak wychodzi 0=0 to ma nieskończenie wiele. Na jedno wychodzi w tym przypadku.

Bogdan: Proponuję przemyśleć jeszcze raz (−3 = −3, ale −3 nie jest mniejsze od −3).

Matematyk: Warte przemyślenia. Spełnia i nie spełnia nierówność. Albo równe jest, albo jest mniejsze. Jest równe, druga opcja odpada, przynajmniej dla mnie. Sprzeczność? Ma ktoś informacje na ten temat? Albo uznajemy, że musi spełniać oba warunki, czyli sprzeczność. Punkt widzenia zależy od punktu siedzenia, albo umawiamy się tak, albo tak To jak się umówili matematycy całego świata?

Bogdan: W matematyce można się umówić w sprawie oznaczeń, ale nie w sprawach merytorycznych dotyczących matematyki. W matematyce po prostu jest i niczego nie przyjmuje się wg czyjegoś widzimisię oraz nie ma punktów widzenia.

Matematyk: Ach... Można polemizować. Poza tym, ta nierówność nie jest sumą rozwiązań "równe" i "mniejsze" od tej wartości. To nonsens.

Matematyk: Jakieś wątpliwości? Jak coś to napisz sensowne rozumowanie, moje jest dość logiczne. A i co do twojej marnej próby obrażenia mnie stwierdzeniem, że mam zmienić nick−moje rozwiązanie było dobre, sprawdzałem wiele razy−trze było tyle narysować wykresy tych funkcji−natomiast twoje było błędne−narysowałeś zły wykres, na dodatek mnie oczerniłeś−zanim napiszesz coś o innych, zastanów się, czy masz prawo.

Bogdan: Matematyku, nie rozumiem ostatniego Twojego tutaj wpisu, domyślam się, że miał on się pojawić w innym miejscu i przez przypadek tu go umieściłeś.

Matematyk: Jest w dobrym miejscu−jest do Ciebie. Kazałeś mi zmienić nick− zadanie z pierwiastkiem z wartości bezwzględnej−sprawdzałem−wypisałeś bzdury, że mam źle(trzeba było tylko porónać te dwie funkcje co napisałem i obliczyć miejsca zerowe−napisałeś jeszcze, że y=√|x+1| to wykres funkcji y=√|x| przesunięty o jeden w prawo, co jest nie prawdą , bo miejscem zerowym jest −1. Reasumując−Zanim coś się napisze, trzeba pomyśleć. Mam do Ciebie wielki szacunek, znasz się na matematyce, ale musisz bardziej uważać nad postami−a ten wieczorny był pisany w afekcie−bo zauważyłem kilka godzin wcześniej twoją pomyłkę, a tu mi jeszcze wyskakujesz z wpisem, że ≥ dla konkretnych liczb(tych samych) jest zła, bo x>x Tego tak się nie rozbija Skończmy to, mnie wydaje się to dziecinne.

Bogdan: Dzień dobry. Proszę tu kliknąć 26395. W zadaniu podana jest nierówność y < √|x − 1|. Po prawej stronie tej nierówności znajduje się wykres funkcji f(x) = √|x − 1|, ale nie nie jest wykres funkcji f(x) = √|x + 1|, jak podajesz.. Cytuję moje słowa tam zamieszczone: "Wykres y = √|x − 1| powstaje przez przesunięcie wykresu y = √|x| w prawo o jedną jednostkę", co niewątpliwie jest prawdą. Dalej cytuję siebie: "Rozwiązaniem nierówności są wszystkie punkty leżące poniżej wykresu y = √|x − 1|", co również jest prawdą. Przypominam tę nierówność: y < √|x − 1|. Nie pisałem więc bzdur, jak twierdzisz. Jeszcze jeden cytat, tym razem Twój: "Zanim coś się napisze, trzeba pomyśleć" − odnieś ten cytat do siebie.

Matematyk: I dobrze, źle zapamiętałem−ale NIE daje ci to prawa do obrażania innych−zgodnie z poprawnymi założeniami moje dwie funkcje opisują właśnie to co ty narysowałeś−z łaski swoje−nie jesteś panem świata! Aktualnie kończę rozmowę z tobą, nie chcesz przyjąć do wiadomości, że bezmyślne pisanie może kogoś dotknąć(zwłaszcza, że zrobił to poprawnie).

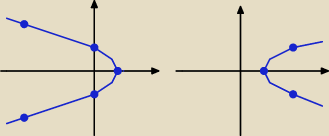
Bogdan: Ja jednak jeszcze wracam do naszej burzliwej rozmowy. Narysowałem zaproponowane przez Ciebie wykresy, które nie są wykresami funkcji. Lewy wykres: y² = −x + 1, prawy: y = x − 1. Te wykresy nie odpowiadają wykresowi funkcji f(x) = √|x − 1|, który przedstawiłem w rozwiązaniu.

Matematyk: Uno momento−tu y jest zawsze dodatnie−ścierasz to pod wykresem(dla y ujemnych) i masz już to. To nie napisałem, że y ma być dodatnie? Cóż, to już można sobie dośpiewać z pierwszego równania. Zabrakło jednego założenia, które odbiorczyni pewnie napisała, a ty wyskakujesz do ludzi z wręcz pogardą−nie wiem, jak to inaczej nazwać. Coś tam chyba napisałem, ze x może być liczbą ujemną−w kontekście że nie zostaje tam to, co napisała autorka, może miałem też na myśli też y−zapomniałem już. Dociera do mnie śmieszność tej sytuacji. Ja się do błędów przyznaję−ani ze mnie matematyk(prawdziwy, jam gimnazjonu nie skończył, jak na ten moment zrobiłem błąd w tym i błąd w obliczeniach w innym, który z BiebrzaFunem poprawiliśmy). Ja mogę napisać, że zadbam o jakość tych rozwiązań