pole czworokąta
Archy:
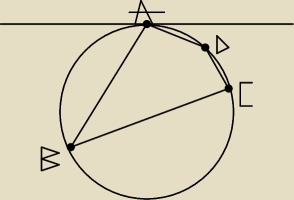
W okrąg o promieniu r wpisano czworokąt ABCD taki, że kąt między styczną poprowadzoną do okręgu
w punkcie A i bokiem AB ma miarę 60 stopni. Wyznacz pole czworokąta ABCD, jeśli BC=2AC oraz
AD=DC
4 lut 12:42
Archy: ?
4 lut 16:36
Tadeusz:
... jak zauważysz i wykażesz, że trójkąt ABC jest prostokątny zatem BC jest średnicą okręgu
to będziesz miał "z górki" −

4 lut 17:51
Jan: Najpierw zauważ, że kąt BCA ma miarę taką samą jak kąt między styczną poprowadzoną do okręgu
w punkcie A i bokiem AB ma miarę 60 stopni. (przestudiuj
4003 i
465 jeśli nei wiesz
skąd się to bierze.)
Następnie wykorzystaj twierdzenie kosinusów w trójkącie BCA, aby wyznaczyć AB, później
twierdzenie sinusów w tym trójkącie, aby wyznaczyć kąt BAC. No i dalej kombinuj

4 lut 18:38
Tadeusz:
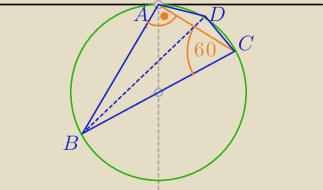
|AB|
2=4|AC|
2+|AC|
2−2*2|AC|*|AC|*cos60
o
|AB|=|AC|
√3
trójkąt o bokach |AC|,
√3|AC| i 2|AC| ... sprawdź Pitagoraskiem −

4 lut 18:38
Archy: nie rozumiem czemu kąt BCA=60...
6 lut 19:17
Archy: dobra już czaje
6 lut 19:22
Archy: tylko stwierdziliście bezpodstawnie że środek boku BC jest środkiem okręgu
6 lut 19:24
Mila:
Dlaczego sądzisz , że bezpodstawnie, bez uzasadnienia, to się zgadzam, ale Tadeusz
podpowiedział, że masz to zauważyć, iż ΔABC jest prostokątny, czy masz z tym problem?
6 lut 20:03
Archy: tak

rozumiem dlaczego kąt BCA ma 60 stopni, ale nie wiem dlaczego CAB ma 90
6 lut 20:55
Mila:
Mam narysować, czy tylko obliczenia napisać?
6 lut 20:58
Archy: obliczenia mi raczej wystarczą
6 lut 20:59
Mila:
Szkoda, że reagujesz za dwa dni, bo miałam rozwiązanie, ale gdy zobaczyłam , że Tadeusz
napisał, to myślałam, że to Ci wystarczy.
Czytam na nowo i zaraz wpiszę.
6 lut 21:02
Tadeusz:
policz z twierdzenia cosinusów |AB| ... i sprawdź Pitagorasem −

6 lut 21:03
Tadeusz:
zresztą ma to napisane 4 lutego o 18:38 .... tylko nie czyta
Trójkąt o bokach 1 √3 2 12+(√3)2=22
6 lut 21:10
Archy: czemu tam jest 4AC?
6 lut 21:12
Tadeusz:
....2*2|AC|*|AC|*cos60o przypomnij sobie twierdzenie cosinusów
6 lut 21:14
Archy: aha ok
6 lut 21:16
Mila:
Korzystając z tego co napisał Tadeusz 18:38
Mamy w ΔABC:
|AC|, |BC|=2|AC|, |AB|=|AC|√3
Stosuję tw. odwrotne do tw. Pitagorasa;
|BC|2=4|AC|2 − kwadrat najdłuższego boku
|AC|2+(|AC|√3|)2=|CA|2+3|AC|2=4|AC|2 ⇔ΔBAC− Δprostokątny
albo twierdzenie cosinusów
(2|AC|2)=|AC|2+(√3|AC|)2−2*|AC|*√3*|AC|*cosA
4|AC|2=4|AC|2−2*|AC|*√3*|AC|*cosA⇔
2*|AC|*√3*|AC|*cosA=0⇔cosA=0⇔A=90o
6 lut 21:18
Archy: dobra dziękuję

ale trzeba mieć łeb żeby to wymyślić

czyli teraz muszę jeszcze wyznaczyć jego pole
6 lut 21:26
Tadeusz:
Policzyć to TY masz pole czworokąta −

6 lut 21:34
Archy: a nie lepiej 2 trójkątów oddzielnie?
6 lut 21:36
Tadeusz:
pewnie że lepiej −

6 lut 21:39
Archy: | | |AC|2√3 | |
no więc pole ABC= |
| , a trójkąt ADC będzie równoramienny, bo w trójkącie ACS |
| | 2 | |
(s−środek) kąty mają po 60 stopni
tylko nie wiem jak wyznaczyć tam wysokość..
6 lut 21:42
Archy: chyba wiem jak to zrobić

trzeba będzie tam coś pokombinować z sinusem i podstawa to będzie r
6 lut 21:46
Tadeusz:
pobaw się kątami −

6 lut 21:46
Tadeusz:
jest prostsza ścieżka −

6 lut 21:47
Archy: a kąt ADC to będzie 150 stopni tak?
6 lut 21:49
Tadeusz:
dlaczego?
6 lut 21:49
Archy: było takie twierdzenie, że jak czworokąt jest wpisany w okrąg to suma przeciwległych kątów to
180 stopni
6 lut 21:50
Archy: dobra poddaje się..
jak to zrobić?
6 lut 21:55
Tadeusz:
przecież jest takie twierdzenie −

6 lut 21:57
Archy: no ale nie wiem co dalej
6 lut 21:58
Archy: help

6 lut 22:02
Tadeusz:
wiesz że trójkąt równoramienny, znasz kąty, znasz podstawę .... to nie rób wsi −

6 lut 22:06
Archy: z tych kątów wyjdą nieładne liczby
6 lut 22:12
Archy: | | 0.2588r | |
wyszło mi w tym trójkącie h= |
| |
| | 2.9318 | |
tak ma być?

6 lut 23:22
Mila:
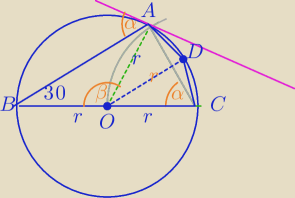
α=60
o
|AC|=r z treści zadania
| | 1 | | r2 | |
PAOCD= |
| *r*r= |
| − pole deltoidu |
| | 2 | | 2 | |
β=120
6 lut 23:45
Archy: skąd taki wzór na pole deltoidu?
6 lut 23:49
6 lut 23:52
Archy: dziękuję
6 lut 23:57
Mila:
7 lut 00:17
 W okrąg o promieniu r wpisano czworokąt ABCD taki, że kąt między styczną poprowadzoną do okręgu
w punkcie A i bokiem AB ma miarę 60 stopni. Wyznacz pole czworokąta ABCD, jeśli BC=2AC oraz
AD=DC
W okrąg o promieniu r wpisano czworokąt ABCD taki, że kąt między styczną poprowadzoną do okręgu
w punkcie A i bokiem AB ma miarę 60 stopni. Wyznacz pole czworokąta ABCD, jeśli BC=2AC oraz
AD=DC


 |AB|2=4|AC|2+|AC|2−2*2|AC|*|AC|*cos60o
|AB|=|AC|√3
trójkąt o bokach |AC|, √3|AC| i 2|AC| ... sprawdź Pitagoraskiem −
|AB|2=4|AC|2+|AC|2−2*2|AC|*|AC|*cos60o
|AB|=|AC|√3
trójkąt o bokach |AC|, √3|AC| i 2|AC| ... sprawdź Pitagoraskiem −
 rozumiem dlaczego kąt BCA ma 60 stopni, ale nie wiem dlaczego CAB ma 90
rozumiem dlaczego kąt BCA ma 60 stopni, ale nie wiem dlaczego CAB ma 90

 ale trzeba mieć łeb żeby to wymyślić
ale trzeba mieć łeb żeby to wymyślić  czyli teraz muszę jeszcze wyznaczyć jego pole
czyli teraz muszę jeszcze wyznaczyć jego pole


 trzeba będzie tam coś pokombinować z sinusem i podstawa to będzie r
trzeba będzie tam coś pokombinować z sinusem i podstawa to będzie r






 α=60o
|AC|=r z treści zadania
α=60o
|AC|=r z treści zadania