trójkąt ABC: W trójkącie ABC na boku AB wybrano punkt M taki, że |AM| : |MB|=2:3. Odcinek MC dzieli środkową AK, licząc od punktu A, w stosunku?

Qulka:

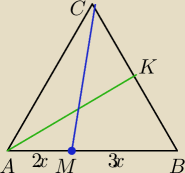
Qulka: za szybko wysłałam równoległą do CM z punktu K da nam na AB punkt D S to przecięcie zielonej z niebieską BD=1,5x

AM		AS
	=
MD		SK

2x		AS
	=
1,5x		SK

więc w stosunku 4:3

clueless: Przepraszam, ale skąd wiadomo, że BD = 1,5x?

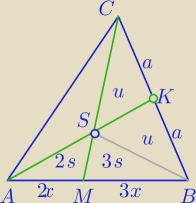Mila: Inny sposób: P=P_ΔABC Małymi literami oznaczono pola odpowiednich Δ. 1) ΔABK:

	1
5s+u=		P
	2

2) ΔMBC:

	3
3s+2u=		P
	5

	2		3
stąd s=		P, u=		P
	35		14

2)

AS		5s		2		3		2		14		4
	=		=(		P): (		P)=		*		=
SK		u		7		14		7		3		3

Eta: https://matematykaszkolna.pl/forum/412132.html