twierdzenie Talesa, trójkąt
clueless: W trójkącie ABC na boku AB wybrano punkt M taki, że |AM| : |MB|=2:3. Odcinek MC dzieli środkową
AK, licząc od punktu A, w stosunku? Wiem, że już ktoś pytał i nawet jest tam rozwiązanie z
twierdzenia Talesa, ale dlaczego BD, gdzie D to punkt na AB wyznaczony przez prostą równoległą
do MC, przechodzącą przez K, miałby się równać 1,5x?
4 gru 16:17
sushi:
jak leży punkt K na odcinku CB ?
4 gru 16:27
clueless: AK jest środkową, K leży w połowie odcinka CB
4 gru 16:32
sushi:
więc punkt D leży pośrodku MB
4 gru 16:37
clueless: To taka własność, twierdzenie? Dlaczego tak jest?
4 gru 16:38
sushi:
TALES
4 gru 16:38
sushi:
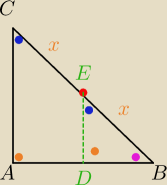
4 gru 16:40
clueless: Dobrze, czyli |AP| : |AM| = |PK| : |MD|. Dalej nie widzę, skąd ta połówka...
4 gru 16:43
clueless: Ooo, jest rysunek!
4 gru 16:44
clueless: Chyba widzę, z podobieństwa trójkątów. Dziękuję za pomoc!
4 gru 16:49
Eta:
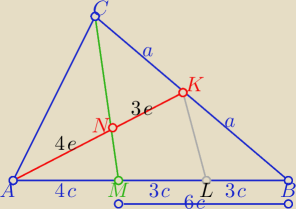
W ΔBCM KL jest środkową
więc |ML|=|LB|=3c i KL || MN
z tw. Talesa
♣♣♣♣♣♣♣♣♣
4 gru 17:53