stereometria magda: Proszę pomóżcie! Dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD i wierzchołku S. Ostrosłup ten przecięto płaszczyzną przechodzącą przez punkty B i D oraz przez punkt P będący środkiem krawędzi CS. Wykaż, że jeśli trójkąt BDP jest równoboczny, to stosunek długości krawędzi bocznej ostrosłupa do długości krawędzi podstawy jest równy 2√3 : √2

Mila: Jest rozwiązane na forum, szukaj.

magda: https://matematykaszkolna.pl/forum/276622.html właśnie znalazłam przed chwilą, ale nadal nie rozumiem jak z tego promienia wychodzi to k?

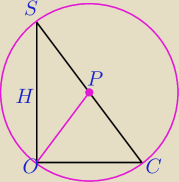
Mila: ΔSOC − Δprostokatny Z treści punkt P jest środkiem SC, a zatem środkiem przeciwprostokątnej. Wiadomo Ci na pewno, że środek okręgu opisanego na trójkacie prostokątnym leży w środku

	1
przeciwprostokątnej i jest równy		c.
	2

Zatem |PC|=|PS| ( z treści)=R to promień okręgu opisanego na ΔSOC. W takim razie OP=R

magda: dzieki