 Witam,
Mam problem z zadaniem z stereometrii. Oto ono:
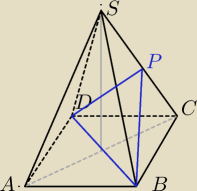
Dany jest ostrosłup prawidówy czworokątny o podstawie ABCD o wierzchołku S. Ostrosłup ten
przecięto płaszczyzną przechodzącą przez punkty B i D oraz przez punkt P będący środkiem
krawędzi CS. Wykaż, że jeżeli trójkąt BDP jest równoboczny, to stosunek krawędzi bocznej
ostrosłupa do długości krawędzi podstawy jest równy 2√3:√2
Nie wiem jak się za to zabrać, pomoże ktoś?
Z góry dziękuję
Witam,
Mam problem z zadaniem z stereometrii. Oto ono:
Dany jest ostrosłup prawidówy czworokątny o podstawie ABCD o wierzchołku S. Ostrosłup ten
przecięto płaszczyzną przechodzącą przez punkty B i D oraz przez punkt P będący środkiem
krawędzi CS. Wykaż, że jeżeli trójkąt BDP jest równoboczny, to stosunek krawędzi bocznej
ostrosłupa do długości krawędzi podstawy jest równy 2√3:√2
Nie wiem jak się za to zabrać, pomoże ktoś?
Z góry dziękuję  !
!
| a√6 | ||
|OP|= | ||
| 2 |
| a√6 | ||
k=SC=2R=2* | =√6a | |
| 2 |
| k | ||
⇔ | =√6 | |
| a |
| k | 2√3 | ||
= | =√6 | ||
| a | √2 |