d
równość: Oblicz pole obszaru D ograniczonego krzywymi:
y = x
2
y = 3x
jakbym miał dwie krzywe to bym wiedział, ale jak jest z trzema. Bo z dwoma zrobiłbym tak:
narysował,odpowiednio przez całkę oznaczoną wykonał działania na tych dwóch krzywych.
Czy dla trzech krzywych jest tak samo tylko po prostu są trzy krzywe ?
30 sty 23:58
Saris: Jest tak samo tylko musisz podzielić obszar na taki, który odzielają tylko 2 krzywe + inne
krzywe (przynajmniej jedna). I liczysz po prostu sumę tych całek oznaczonych (na różnych
przedziałach). Jak narysujesz sobie, bo to łatwe wykresy to widać.
31 sty 00:03
Godzio:
| | 1 | | 1 | |
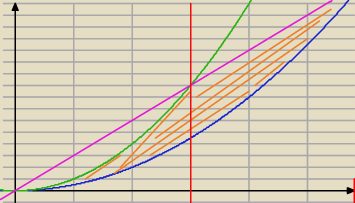
P = ∫03(x2− |
| x2)dx + ∫36(3x − |
| x2)dx = ... |
| | 2 | | 2 | |
Rozbijasz obszar na dwa pola.
31 sty 00:04
równość: myślałem że zaznacza się jedno pole tak jak w dwóch krzywych. Tutaj są 3 pola ?
31 sty 00:08
Saris: Te proste ograniczają tylko 1 kawałęk płaszczyzny, więc skąd 3 pola? Po prostu nie wszystkie
naraz ograniczają cały obszar tylko na przedziałach. Rozumiesz?
31 sty 00:12
Saris: tam powinien być przecinek przed tylko.
31 sty 00:12
równość:
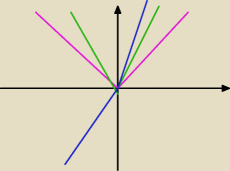
coś w podobie tego wyszedł mi rysunek, tylko te linie mieli być takie bardziej wypukłe ale nie
wiedziałem jak je tak narysować. Dobrze jest ? Bo nie wiem gdzie te pole zaznaczyć.
31 sty 03:00
równość: ?
31 sty 07:41
Janek191:
Masz niżej program do rysowania wykresów funkcji − kliknij na rysuję
31 sty 07:58
Janek191:
Masz niżej program do rysowania wykresów funkcji − kliknij na rysuję
31 sty 07:59
równość: robiłem nim ale nie wiem jak tam narysować takie wypukłe linie ?
31 sty 08:13
równość:
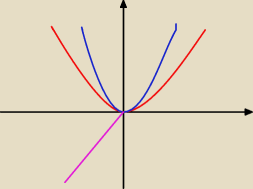
ok jest?
31 sty 09:02
Eve:
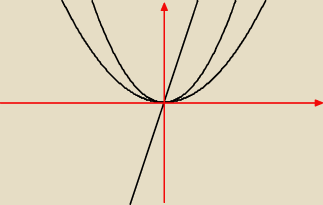
31 sty 09:23
równość: czyli ok, bo mi tak wyszło, tylko nie wiem gdzie zaznaczyć to pole.
31 sty 09:28
Eve: 1 i 3 funckja mają wspólny punkt (0,0) i (3,9)
2 i 3 − (0,0) i (6,18)
masz post 00.04
31 sty 09:32
równość: i teraz już te pole co mam to trzeba obliczyć odpowiednio pierwszą całkę oznaczoną i drugą
oznaczoną i dodać ?
31 sty 10:14
Eve: tak
31 sty 10:16
31 sty 10:19