x^2-kx+k+3 mniejsze od 0 - jak to ugryźć? Marek: Dla jakich wartości parametru k nierówność jest spełniona dla każdego x∊R ? x²−kx+k+3 mniejsze od 0 Jak to się rozwiązuje? Wiem, że : a≠0 a Δ?

Marek: Chyba: Δ musi być mniejsza od 0 a musi być większe od 0 a co dalej?

J: ..nie ma takiej wartości k .....

5-latek: Witaj J Marku po co zakladasz ze a>0 ? Przeciez juz w rownaniu masz to

J: Witaj ...

Kacper: Dobry Tak to jest jak się uczy warunków "na blachę"

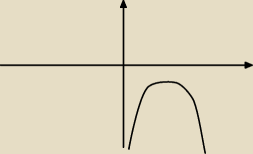
Krystek: Masz mieć taką sytuację, czy ona jest możliwa gdy a=1?

Krystek: https://matematykaszkolna.pl/strona/79.html

Marek: Dziękuję, widzę , że to niemożliwe. Matematyki uczyłem się ponad 30 lat temu, niestety, okazuje się że mało pamiętam.

Krystek: Ale przypomnisz sobie, wówczas matematyka stała na wyższym poziomie niż obecnie!

Marek: Dla jakich wartości parametru k nierówność jest spełniona dla każdego x∊R ? x²−kx+k+3 większe od 0 Dla wszystkich, bo parabola nie ma punktów stycznych z osią OX, tak?

Kipic: Wydaje m isię ze takie cos wyjdzie

Marek: W drugim zadaniu wydaje mi się, że warunkiem koniecznym jest aby Δ<0 Czyli dobrze myślę? Wtedy należy rozwiązać nierówność: k ²−4(k+3) <0 Czy to rozumowanie jet OK?

J: w tym przykładzie ..tak , Δ < 0

Krystek: ok