ekstremum funkcji xxx: Oblicz ekstremum funkcji y=x+x⁻¹ . Obliczyłem pochodną = 1−1/x² ale nie wiem co dalej

john2: Wyznacz dziedzinę f(x) i f'(x). Rozwiąż równanie f'(x) = 0 Zbadaj znak pochodnej. https://matematykaszkolna.pl/strona/387.html

Mila: 1) D_f=R\{0}

	1
2) f'(x)=1−		⇔
	x2

	x2−1
f'(x)=
	x2

f'(x)=0⇔ x²−1=0 x=1 lub x=−1 − kandydaci na ekstrema 3)

	x2−1
f'(x)>0⇔		>0⇔x2−1>0 i x∊Df'⇔
	x2

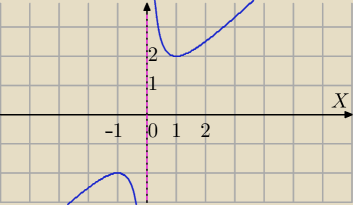
x<−1 lub x>1 ⇔f(x)↑dla x∊(−∞,−1) f(x)↓ dla x∊(−1,0) , f(x)↓ dla x∊(0,1) ⇔dla x=−1 f(x) ma maksimum lokalne, f(−1)=−1−1=−2 f(x)↑ dla x∊(1,∞) ⇔dla x=1 f(x) ma minimum lokalne f(1)=2 ( zapisy przedziałów napisz jak Cię uczą, chodzi mi o domknięcia przy monotoniczności) Jeszcze masz pytania?

PW: A dla przypomnienia: szukanie ekstremów jest inną wersja znanego szkolnego zadania

	1
a +		≥ 2
	a

dla a > 0 (jest też wersja dla a <0), w liceum rozwiązywanego za pomocą funkcji kwadratowej albo nierówności między średnimi. Ładny przykład na różne rozwiązania tego samego zagadnienia.