R3 Lukas: Pomoże ktoś z geometrią w R3 ? Wektory u, v , w są bazą pewnej przestrzeni liniowej V. Sprawdzić czy wektory 5u+5v+w, 2u+2v+w, u+v−w są liniowo niezależne .

Lukas: Mila ?

zombi: (5u+5v+w) + (−2)(2u+2v+w) − (u+v−w) = (0,0,0) wniosek?

Gray: Oblicz wyznacznik macierzy: 5 5 1 2 2 1 1 1 −1 Wyznacznik równy zero, są zależne; różny od zera, są niezależne.

Lukas: Ale możecie mi wytłumaczyć co z czym się je ?

zombi: Byłby liniowo niezależne jeśli chociażby z warunku a(5u+5v+w) + b(2u+2v+w) +c(u+w−v) = (0,0,0) wynikałoby, że a=b=c=0 (jedyna możliwość, ale ja wskazałem takie a,b,c ≠ 0, że warunek nasz zachodzi. Wniosek? Są liniowo zależne.

Lukas: Panowie pomożecie jeszcze ?

Lukas: Dla jakiej wartości p układ jest układem cramera x+y+z+6 x+y−z=0 2x+3py+pz=−7 1 1 1 1 1 −1 2 3p p i liczę z tego wyznacznik ?

Saris: układ cramera ⇔ układ oznaczony ⇒ det A≠0

Lukas: sprawdzić dla jakiej wartości parametru p punkty A=(1,1,1) B=(2,3,2) C=(2,2,4) D=(p,1,1) są współpłaszczyznowe ?

Lukas: ?

Lukas: ?

Mila: AB^→=[1,2,1] AC→=[1,1,3] AD^→=[p−1,0,0] 1 2 1 1 1 3 p−1 0 0 Iloczyn mieszany wektorów W=−p+6(p−1)+1 W=0 ⇔p=1 Opd. dla p=1 punkty są współpłaszczyznowe. (objętość czworościanu ABCD jest równa 0)

Lukas: objętość czworościanu ? Mogę prosić o wytłumaczenie zadania bo nie bardzo wiem co tutaj robić ?

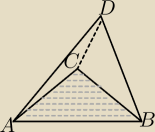
Mila: Jeżeli połączysz 4 punkty niewspółpłaszczyznowe to otrzymaszz ostrosłup trójkątny ( inaczej czworościan) Objętość czworościanu liczymy wg wzoru:

	1
V=		*||(AB→xAC→)oAD→||
	6

Tu liczysz wyznacznik W: Jeżeli W=0 to oznacza, że punkty A,B,C,D leżą w jednej płaszczyźnie. Poczytaj wykłady.

Gray: Można też na to popatrzeć w ten sposób: cztery punkty A,B,C,D z R³ leżą na jednej płaszczyźnie wtedy i tylko wtedy, gdy trzy wektory utworzone z tych punktów tj. AB, AC, AD są liniowo zależne. Ten warunek zachodzi, gdy wyznacznik macierzy utworzonej z tych wektorów jest równy zero.

Lukas: Dziękuję a mogę jeszcze prosic o pomoc ?

Lukas: nadal nie rozumiem czemu Pani Mila liczy tutaj objętość tego czworościanu ?

Mila: Wciśnij D do podstawy, to będzie Δ i objętość równa się 0, a punkty leżą w jednej płaszczyźnie. To jest to samo o czym pisze Pan Gray.

Lukas: Ale Pan grey piszę, że można policzyć tylko wyznacznik macierzy a Pani liczy iloczyn mieszany wektorów +objetośc, w książce nie moge odszukac odpowiedzi na moje pytanie, podane tylko jak liczyc obejetośc czworoscianu

Lukas: ?

Mila: Też liczę wyznacznik. Przecież masz napisaną macierz i jej wyznacnik pod spodem.

Saris: 1. iloczyn mieszany to wyznacznik macierzy zlozonej z tych 3 wektorów 2. iloczyn mieszanin 3 wektorów rozpinających czworościan reprezentuję jego objętość. V=0, brak czworościana ⇔ punkty leżą na jednej płaszczyźnie.

Lukas: dziękuję teraz zrozumiałem, dobrej nocy

Mila: Saris, to proszę Cię na odsiecz tu: https://matematykaszkolna.pl/forum/276395.html