Trochę zadań z okręgami Bambi: Dane są pkt A(−1,5) B(2,−4) C(8,2) Wykaż że jest równoramienny. Trzeba obliczyć wszystkie długości boków po kolei. A(−1,5) |AB|=√(−1−2 )² + (5−(−4))² |AB|=√(−3)²+9² |AB|=√90=3√10 |BC|=√(2−8)²+(−4−2)² |BC|=√(−6)²+(−6)² |BC|=√72=6√2 |CA|=√8−(−1))²+(2−5)² |CA|=√9²+(−3)² |CA|=√90=3√10 Więc trójkąt jest równoramienny. Wykaż że czworokąt ABCD jest równoległobokiem A(−4,1) B(5,−2) C(7,2) D(−2,5) Zrobimy to na wektorach. Można to też tak jak tutaj zamieszczone jest, liczyć współczynnik kierunkowy i czy wyjdzie takie samo "a". https://matematykaszkolna.pl/forum/149809.html Warto narysować sobie mniej więcej ten czworokąt żeby wiedzieć które boki przyrównywać, bo może zdarzyć się np w tym przypadku że ktoś będzie porównywać AD do DC i wtedy tylko robota na marne. Warto też przypomnieć sobie definicje równoległoboku:" Dwie pary prostych równoległych" Więć AD || CB i DC||AB żeby był równoległobokiem. Sprawdźmy więc czy wektor AD i wektory CB ma taką samą wartość AD→ (D_x−A_x, D_y−A_y) = (−2−(−4),5−1)=(2,4) taką samą metodą CB→ = (2,4) Więc AD||CB Teraz druga para: DC→ = (9,−3) AB→ = (9,−3) Więć DC||AB ⇒ ABCD jest równoległobokiem Oblicz długość boku trójkąta równobocznego ABC, A(2,1−P{2}), zaś S(−3,1) jest środkiem okręgu opisanego na trójkącie. Obędzie się bez rysunku w tym zadaniu. Na samych wzorach to zrobimy

	2
R=		h
	3

	a√3
h=
	2

	2		a√3		a√3
R=		*		=
	3		2		3

Obliczmy zatem R. Wiadome że R to odległość środka do wierzchołka. Nie rozumiesz narysuj sobie i sam zobacz ! |SA|=√(2+3)²+(−√2)² |SA|=√27=3√3 mamy nasz promień

	a√3		3
3√3=		/
	3		√3

a=9

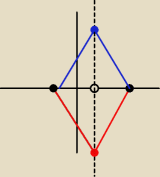
Bambi: PKT A(−3√3,0) B(5√3,0) są wierzchołkami trojkąta równobocznego. Wyznacz C Liczymy odległość z A do B Widać odrazu że będzie to 3√3 + 5√3 = 8√3. Ponieważ od Pkt A do Pkt (0,0) jest |−3√3| 8√3 : 2 = 4√3 Dzielimy na dwa ponieważ KAŻDA wysokosć w trojkącie równobocznym dzieli bok na połowy. 5√3−4√3=√3 − to jest współrzędna x ! Narysuj ten rysunek żebyś wiedział jak to wygląda Mamy taki o to trójkąt, ponieważ będą DWA rozwiązania spełniające warunki zadania.

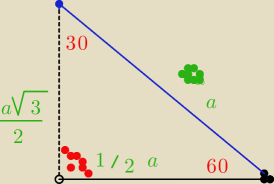
Bambi: Te zielone kropki to bład c.d z załeżności trójkąta o kątach 30/60/90

	1
mamy		a wiemy że u nas to jest 4√3. Zobacz rysunek i zrozum dlaczego tak jest !
	2

	1
więć		a=4√3
	2

	a√3
liczymy		=
	2

	1
więc		a=4√3 /*2
	2

więc a=8√3

	a√3		√3
		=8√3*		=12
	2		2

Więc nasza długosć wysokości = 12 ! Ale to jest długość, nie współrzędna, patrz rys. 1 Musimy od naszego pkt (√3,0) odmierzyć 12 na prostej przechodzącej przez pkt (√3,0) czyli y₁=12 y₂=−12