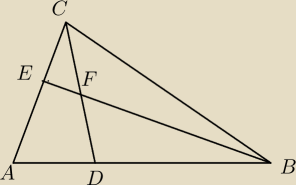
W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |D Danuta: W trójkącie ABC punkty D, E leżą odpowiednio na bokach AB i AC tak, że |AD| : |DB| = 1 : 2 oraz |AE| : |EC| = 2 : 1. Wyznacz jaką część pola trójkąta ABC stanowi pole czworokąta ADFE.

hanna:

a7: https://matematykaszkolna.pl/forum/280787.html

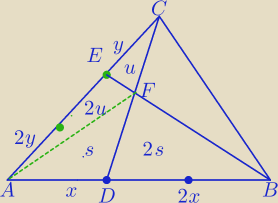Mila: Krócej niż w linku: P_ΔABC=P

	2		1
1) PΔAEB=		P=2u+3s , PΔADC=		P=3u+s
	3		3

================= 2)

	2
2u+3s=		P
	3

	1
3u+s=		P⇔
	3

	4		1
s=		P, u=		P
	21		21

3)

	4		2		6
PADFE=		P+		P=		P
	21		21		21

	2
PADFE=		P
	7

===============