trygonometria
adam:
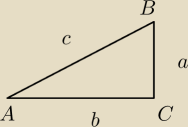
wiem, że sinus to przeciwległa przyprostokątna do przeciwprostokątnej
oraz wiem, żc C jest równe 15
| | a | |
ogólny wzór na sinusα w tym przypadku mam taki sinα = |
| |
| | c | |
, ale jak to zrobić aby policzyć boki a,b,c, może ktoś mnie nakierować?
24 sty 20:28
adam:
Dane : c = 15
24 sty 20:29
Eve: no to podstaw za c i sin, obliczysz a, potem np z tw. Pitagorasa
24 sty 20:30
adam: ściana
, za co mam podstawić?
24 sty 20:33
5-latek: | | a | |
Przeciez sam napisales ze sinα= |
| Wyznacz z tego wzoru a |
| | c | |
24 sty 20:37
Eve: | | 3 | |
adam sinα= |
| , c=15, wstaw do wzoru, to na pewno potrafisz, do wzoru na sinα |
| | 5 | |
24 sty 20:40
adam: c* sinα = a
a = c*sinα
już chyba rozumiem
teraz liczę
a=9
z tw.Pitagorasa
a
2+b
2=c
2
9
2 + b
2 = 15
2
81+b
2= 225
b=
√144
b= 12
to odp; a=9, b=12=c=15
24 sty 20:41
Eve: | | 3 | | a | |
a mówiłam, że potrafisz  można tak: |
| = |
| i lecisz proporcją |
| | 5 | | 15 | |
24 sty 20:42
5-latek: Eve Prosze zobacz tutaj bo tego dzialu nie trawie
dzieki
24 sty 20:43
24 sty 20:43
adam: mam teraz trudniejszy przykład do tego samego rysunku, a mianowicie
a=14
tutaj tak samo wyznaczam c, albo b? tylko, że posiadam wartość boku A, natomiast ani b ani c
nie mam
24 sty 20:47
Eve: spojrzałam, tez tego nie trawie , tfuuuuu
24 sty 20:51
Eve: a tożsamości trygonometryczne znasz?
24 sty 20:52
5-latek:
dziekuje Ci
24 sty 20:53
adam: wydaje mi się, że znam, ale nie bardzo wiem jak do tego praktycznie podejść
24 sty 20:53
Eve: jedynka trygonometryczna, napisz wzór
w której jesteś klasie?
24 sty 20:54
adam: sinα2 + cosα2 = 1
pierwsza, nie mam ścisłego umysłu do takich rzeczy
24 sty 20:56
adam: miało być sin2α = cosα = 1
24 sty 20:59
adam: sin2α + cos2α = 1
24 sty 20:59
Eve: no to podstaw na sinus ułamek, który masz oblicz cosinus
24 sty 21:01
24 sty 21:03
adam: chyba się pomyliłem, bo powinno być
cos
2β = {1}{49}
co dalej?
24 sty 21:11
Eve: odwrotnie
1−sin
2α=cos
2α
| | 7 | | a | | 14 | |
więc cosα= |
| = |
| = |
| |
| | 25 | | c | | c | |
policz c
24 sty 21:13
adam: fakt pomyliłem się, bo
cosβ *c = a /:cosβ
i z pitagorasa
a
2+b
2=c
2
14
2+b
2=50
2
b
2 = 2500 − 196
b=48
już chyba zaczynam powoli łapać te operacje na tożsamościach
24 sty 21:26
Eve: świetnie
24 sty 21:27
adam:
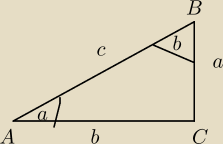
mam taki przykład,
b =
√6 +
√2
tgβ = 2+
√3
ale nie widzę za bardzo wyjścia z problemu,. chciałbym użyć jedynki trygonometrycznej , ale nie
widzę zastosowania, jakieś wskazówki?
24 sty 21:33
adam: może take coś
ale nadal nie potrafię ruszyć do przodu
24 sty 21:38
adam: aaa chyba wiem, teraz
24 sty 21:40
5-latek: napisz tu definicje tngensa
24 sty 21:41
Eve: a skąd ci to wyszło?
nie, to sie robi inaczej
24 sty 21:42
5-latek: O to wlasnie chodzilo
24 sty 21:42
adam:
przyprostokątna leżąca na przeciw kąta do drugiej przyprostokątnej
24 sty 21:43
Eve:
| | b | | √6+√2 | |
tgα=2+√3= |
| ⇒2+√3= |
| |
| | a | | a | |
i teraz z proporcji liczysz a
24 sty 21:44
adam: | | 6+√2 | | 2−√3 | |
a = |
| * |
| = 12 − 6√3+2√2−√6 |
| | 2+√3 | | 2−√3 | |
24 sty 21:47
Eve: dobrze, uporządkuj
24 sty 21:49
Eve: nie, wróć, zgubiłeś pierwiastek przy 6
24 sty 21:50
adam: no nie widze gdzie
24 sty 21:53
Eve: ale jak poprawisz to będzie dobrze
24 sty 21:55
adam: aaa tutaj,
| √6+√2 | | 2−√3 | |
| * |
| = 2√6−√18+2√2−√6=√6−3√2+2√2= √6 − √2 |
| 2+√3 | | 2−√3 | |
24 sty 21:59
Eve: dobrze
24 sty 22:00
adam: mam inny przykład
tgα = 1,5
c = √13
nie bardzo wiem jak zacząć
24 sty 22:01
24 sty 22:02
Eve:
z tw. Pitagorasa c
2=a
2+b
2
24 sty 22:03
adam: to tak:
(√13)2 = 32 + 22?
24 sty 22:05
Eve: dobry jesteś, od razu masz a i b
a wiesz jak to rozwiązać, jakby liczby były inne?
24 sty 22:06
adam: no to weźmy na przykład tgα = 2,
| | a | |
tgα = |
| , w takim razie a jest = 2, a b = 1  |
| | b | |
24 sty 22:07
Eve: nie, podaj jeszcze jakieś c
24 sty 22:08
adam: może to zły przykład z tgα=2 , bo muszę mieć tr. prostokątny, gdyż z tw. pitagorasa a
2+b
2
musi być równe c
2
a c = 5
24 sty 22:10
Eve:
tgα=2⇒ a=4, b=2 prawda?
24 sty 22:10
adam: tak
24 sty 22:11
Eve:
a dlaczego dla a=2 i b=1 nie można mieć prostokątnego? c=√5
24 sty 22:12
adam: c wtedy musi być równe √20
24 sty 22:12
adam: @eve, aa pomyliłem się, coś mi się ubzdurało (22:10),
24 sty 22:13
Eve: tak, ale teraz odwrotnie, jak masz c a nie masz a,b tylko tg? wiesz jak skorzystać z tej
proporcji z poprzedniego zadania?
24 sty 22:13
adam: @Eve
dzięki , że zwróciłaś mi na to uwagę
24 sty 22:13
adam: no chyba wiem,
rzuć mi jakiś przykład
24 sty 22:14
Eve:
22.03 rozwiąż, bez zgadywania
24 sty 22:15
adam: a= 3 b=2, c =√13
z pitagorasa liczyłem a2+b2=c2
24 sty 22:17
Eve: nie, zgadłeś, że a=3, b=2
24 sty 22:20
Eve: tgα=1, c=6√2 znajdź a i b
24 sty 22:23
adam: | | 15 | |
z 22.03 mam tgα= |
| , , aa pytanie było o a i b , tak? |
| | 10 | |
| | 3 = a | |
to tgα= |
| , czy może ja czegoś nie zrozumiałem |
| | 2 = b | |
24 sty 22:24
adam: ok już szukam
24 sty 22:24
Eve: zobacz poprzedni post i oblicz a i b
24 sty 22:24
adam: już rozumiem co miałaś na myśli
(6
√2)
2 = a
2 + b
2
czy tgα=1 oznacza, że jest to tr. 45,45,90?
a
2+a
2 = (a
√2)
2
2a
2 = (6
√2)
2
2a
2 = 72
a
2 = 31
a= b =
√31 ?
24 sty 22:30
Eve: a
2=36
24 sty 22:34
adam: a2 = 36
a=b=6
24 sty 22:34
Eve:
| | a | |
można łatwiej, |
| =1⇒a=b |
| | b | |
72=a
2+a
2
72=2a
2 itd
| | a | | 3 | | 3 | |
z poprzedniego |
| = |
| ⇒a= |
| b |
| | b | | 4 | | 4 | |
24 sty 22:36
adam: no dobra, wrócę jeszcze do 22.03
mam tgα=1,5
a c= √13
czy chodzi o ot, że (a{p})2 + a2 = 2a2?
24 sty 22:40
adam: (a√3)2 + a2 = 2a2?
24 sty 22:41
Eve: | | 3 | |
nie, chodzi o to, że a= |
| b |
| | 2 | |
24 sty 22:42
Eve: poza tym (a√3)2+a2= 4a2
24 sty 22:44
adam: aha , już rozumiem , dziękuję za wszystko
24 sty 22:45
Eve: cieszy mnie to, że chciałeś zrozumieć, trygonometria nie jest łatwa, dlatego podstawy robię już
w gimnazjum, potem uczniowie maja łatwiej
24 sty 22:46