asd aleksandra: Zbadać przebieg zmienności funkcji:

	12x
f(x)=−
	x2 + 9

Dawid: Czego nie wiemy ? Policz pierwsza pochodną

aleksandra: nic właśnie nie wiem

Dawid: A znasz wzory na pochodne ?

Dawid: Zacznij może od wyznaczenia dziedziny.

aleksandra: nie cały ten dział mam w plecy

Dawid: Wyznaczanie dziedziny było w gimnazjum ?

Dawid: Więc wiedza z studiów do tego nie jest potrzebna

aleksandra: Df=R

aleksandra: mówiłam o wzorach

Dawid: No to teraz liczymy pierwszą pochodną Pomogę Ci

	(−12x)'(x2+9)−(−12x)(x2+9)'
f'(x)=		=
	(x2+9)2

oblicz dalej sama korzystając z tych wzorów https://matematykaszkolna.pl/strona/359.html

aleksandra: no i juz nie wiem z ktorego mam skorzystac

aleksandra:

−12x
x2+9

Dawid: Po kolei (−12x)'=... Wzór: (ax)'=a (x²+9)' Korzystasz z tego jak masz dodawanie to można rozbić na dwie pochodne (x²)'+(9)'=... Wzory: (xⁿ)'=nxⁿ⁻¹ (c)'=0 C to stała Mając wzory dokończ

aleksandra: CO JA MOWIE

aleksandra:

−12x2−108x+108
x4+81

aleksandra: jak to jest zle, a pwnie jest, to nie mam pojecia jak to zrobić

Dawid: Mianownik zostaw tak jak jest nie ruszamy go. Policzmy licznik: (−12x)'(x²+9)−(−12x)(x2+9)'=−12(x²+9)−(−12x)(2x)=−12x²−108+24x²=12x²−108=12(x²−9)

Dawid: Rozumiesz?

Dawid:

	12(x2−9)
Zatem pierwsza pochodna to f'(x)=
	(x2+9)2

aleksandra: jak na razie tak

Dawid: Teraz pochodną przyrównujesz do zera i rozwiązujesz

aleksandra: √3

Dawid: Skąd ?

aleksandra: tak mi wyszlo jak przyrownalam do zera

Dawid: Pokaż jak to robisz

Marcin: Pochodna jest równa zera ⇔ licznik = 0.

aleksandra:

	12
skróciłam, zostało
	x2+9

aleksandra: nie no to jest bez sensu bo to prawie to samo co w tresci zadania −.−

Dawid: od kiedy można tak skracać ? to nie jest to samo

12(x2−9)
	=0/*(x2+9)2 Zał: (x2+9)2>0
(x2+9)2

Dokończ

Marcin: Nie możesz tak skracać. W liczniku masz odejmowanie, a w mianowniku dodawanie.

aleksandra: o kurde, faktycznie

aleksandra: −177 haha

Dawid: To ile Ci wyszło ?

aleksandra: √−177

Dawid: Jak tak Ci to wychodzi pokaż ?

Marcin: że co?

aleksandra: 12(x²−9)=(x²+9)²

5-latek: A przebieg zmiennosci funkcji to jest w liceum czy na studiach ?

aleksandra: 12x²−108=x⁴+81

Marcin: W 'starym' programie w szkole średniej na pewno nie było. Teraz to nie mam pojęcia, bo dużo się zmieniło

aleksandra: na studiach

Dawid: Skąd ten kwadrat? 12(x²−9)=0 12(x−3)(x+3)=0 Zatem ?

Marcin: aleksandra − kompletnie nie tak.

5-latek: No to ladnie Olu

aleksandra: no a co z prawą stroną?!

Dawid: 0*(x²+9)²=0

aleksandra: juz mam ten egzamin w plecy :x

Marcin: Jeżeli masz mianownik i chcesz wyznaczyć jego miejsca zerowe, to musisz sprawdzić kiedy licznik jest równy zero i ew. czy argument dla którego licznik = 0 nie zeruje mianownika.

5-latek: a Olu 0* cos tam = ile ?

aleksandra: no ok i co dalej Dawid?

aleksandra: 3 i −3

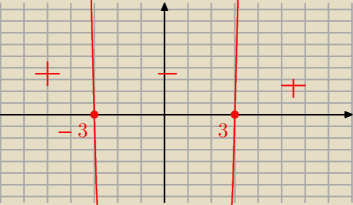
Dawid: Teraz prostsza metodą wytłumaczę rysujesz wykres tej postaci 12(x−3)(x+3)=0 miejsca zerowe x=3 v x=−3 Zatem wykresem takiej funkcji jest parabola Ramiona skierowane do góry bo współczynnik przy najwyższej potędze jest >0 Potem zaznaczasz gdzie funkcja przyjmuje wartości dodatnie a gdzie ujemne Czyli to co jest pod osią OX przyjmuje wartości ujemne a to co nad osią wartości dodatnie. Więc z wykresu można odczytać, że: f(x)↗ dla x∊(−∞,−3)u(3,∞) f(x)↘ dla x∊(−3,3)

aleksandra: czyli to byla monotonicznosc?

aleksandra: no ok i co dalej

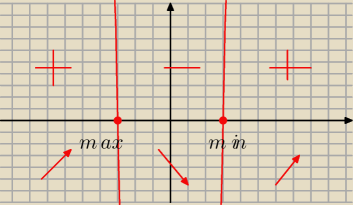
Dawid: Tak i jeszcze do tego musimy policzyć ekstrem, czyli minimum i maksimum, korzystamy z tego rysunku. Tam gdzie plus to strzałka do góry gdzie minus strzałka w dół. I widać że jak mamy ↗↘ to tam jest max a jak jest ↘↗ min Więc teraz wystarczy obliczyć gdzie osiąga minimum a gdzie maksimum. F_max(−3)=... F_min(3)=... Podstawiasz do pierwotnej funkcji za x 3 i −3 i wychodzi Ci y

aleksandra: 2 i −2

Dawid: No tak

aleksandra: no i co dalej

Dawid: Dużo tego jest Poszukaj punktów przecięcia z osią OX i OY podstaw pod x=0 potem pod y=0 i otrzymasz miejsca przecięcia z osiami

aleksandra: OX= 0?

Dawid: Z osią OX i OY ten sam punkt jest przecięcia (0,0)

aleksandra: i OY tez

aleksandra: chociaż z tego rysunku tak nie wynika

Dawid: Tak wygląda wykres

aleksandra: a no chyba ze

aleksandra: a przykład wklęsłości i wypukłości

Dawid: teraz policz sobie punkty przegięcia. Liczysz drugą pochodna. Masz pierwszą pochodną to policz teraz pochodną tej pochodnej czyli drugą pochodną. Następnie ją też przyrównujesz do zera i rysujesz wykres. Bardzo podobnie jak wcześniej

Dawid: punkty przegięcia oraz wklęsłość i wypukłość policzysz z drugiej pochodnej

aleksandra: no tylko ze nie wiem jak sie liczy 2 pochodna

Dawid: tak samo jak pierwsza

aleksandra: a musze pierw przemnozyc 12 przez nawias?

Dawid: możesz

aleksandra:

(12x2−108)'*(x2+9)2−(12x2−108)*(x2+9)2'
x2+92)2

Dawid: Dokładnie

aleksandra:

12(x2+)2−(12x2−108)2x
(x2+92)2

aleksandra: +9 tam mialo byc

Dawid:

−24x(x2−27)
(x2+9)3

aleksandra: jak to zrobiles