ekstrema funkcji Klaudia: Jakie są ekstrema funkcji y=−1−x⁽2/3). Mi wychodzi, że nie ma a na wolframalpha jest że x=0 jest max.

J: jesli ta funkcja to: f(x) = −1 −x^2/3 .. to nie ma ekstremum ...

Klaudia: Też tak myślę, to czemu na wolframalpha jest inaczej?

J: tego nie wiem ... pochodna się przecież nie zeruje..

Janek191: Dla x = 0 funkcja przyjmuje największą wartość , ale nie ma maksimum.

Klaudia: Te 0 to chyba nawet nie jest punkt przegięcia bo 0 nie należy do dziedziny pochodnej 1 i 2 rzędu. Mam rację? I jeszcze jedno tą wartość największą wziąłeś z wykresu czy ją jakoś obliczyłeś?

Klaudia: Ale przecież funkcja ta nie ma największej wartości

Janek191: Dla x = 0 jest y = − 1 , a funkcja jest malejąca.

Klaudia: z lewej strony od x=0 też jest malejąca

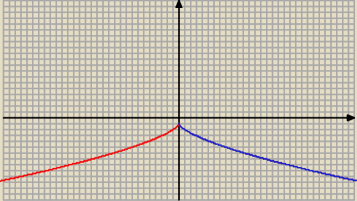
Janek191: Dokończę: jest malejąca dlx x > 0 i rosnąca dla x < 0 .

Klaudia: http://www.wolframalpha.com/input/?i=-1-x%5E%282%2F3%29

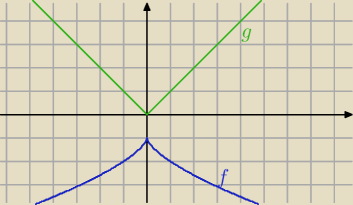
Mila: W punkcie x=0 nie istnieje pochodna f(x)=−1−³√x². W przypadku, gdy nie istnieje pochodna w pewnym x₀ to może istnieć ekstremum, jeżeli x₀ ∊D_f. Takim prostym przykładem jest np. g(x)=|x|.

john2: Wpadłem kiedyś w podobną pułapkę. Polecam ten wątek https://matematykaszkolna.pl/forum/271957.html

Mila: john Nie widziałam tego wpisu, ale to samo napisałam.

john2: Fakt