analiza kyrtap: Znajdź równanie stycznej do wykresu funkcji y = xlnx równoległej do osi Ox.

kyrtap: wiem że muszę policzyc pochodną y i że oś ox ma równanie y = 0

Gray: Znajdź punkt x₀>0 dla którego f'(x₀)=0. f'(x₀) to współczynnik kierunkowy stycznej do f w x₀.

kyrtap:

	1
znalazłem x =
	e

kyrtap: czyli

	1		1
f'(		) = ln		+ 1 = logee−1 = −1 + 1 = 0
	e		e

kyrtap: Gray dobrze?

kyrtap: Mój mistrzu?

kyrtap: ?

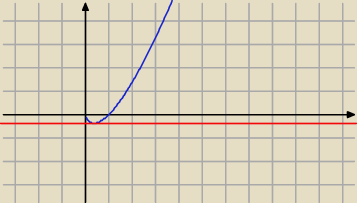
Mila: f(x)=xlnx f'(x)=1+lnx 1+lnx=0

	1
x=
	e

	1		1		1		1
f(		)=		ln		=−
	e		e		e		e

	1
s: y=−
	e

kyrtap: Kochana Mila ile razy już pomogłaś mi?

Mila:

kyrtap: Milu teraz takie zadanie wykazać że funkcja y = x³ + x² + x +1 jest rosnąca liczę pochodną y' = 3x² + 2x + 1 liczę Δ = 4 − 4 * 3 <0 ⇒ funkcja jest rosnąca na R dobrze?

bezendu: ja w środę mam z tego kolokiwum

kyrtap: ja jutro

Saizou : może nie jestem Mila ale jest ew. bez delty 2x²+x²+2x+1=2x²+(x+1)²

kyrtap: dzięki wielkie Saizou szybko chcę przelecieć najważniejsze rzeczy czy coś nie wyleciało mi z głowy

Saizou : Patryk https://matematykaszkolna.pl/forum/274660.html

Mila: Patryk dopisać: f'(x)>0 dla x∊R⇔f(x) −funkcja rosnąca

Gray:

kyrtap: rozumiem Milu

Mila: Gray, dlaczego robisz mi zimny(?) prysznic?

Gray: Milu, dlaczego zimny?

kyrtap: Moi kochani eksperci jak policzyć regułą pana Hospitala

	xn
limx→∞
	ex

kyrtap:

	∞
wiem że będzie nieoznaczoność [		]
	∞

liczę pochodną licznika i mianownika

	nxn−1
limx→∞ =		i dalej nic nie wynika
	ex

kyrtap: ?

kyrtap: ktoś wie?

kyrtap: proszę o rozwiązanie go jutro mam koło z tego

Mila: n≥1 liczysz kolejne pochodne w liczniku i mianowniku: w liczniku otrzymasz : n*(n−1)*(n−2)..1 czyli stałą W mianowniku zawsze e^x.

kyrtap: a czemu Milu założyłaś że n≥1

kyrtap:

Gray: Czym jest n? Mila założyła (całkiem naturalne to założenie), że jest liczbą naturalną. Gdyby liczba n nie była liczbą naturalną, postępujesz tak samo, tylko liczysz [n]+1 pochodnych, tj. tyle aż po raz pierwszy w wykładniku x^? pojawi się liczba mniejsza od zero. Wtedy kończysz stwierdzając, że granica to 0. Np.

xπ		xπ−1		xπ−2		xπ−3
	=H π		=H π(π−1)		==H π(π−1)(π−2)		=H
ex		ex		ex		ex

	xπ−4
=π(π−1)(π−2)(π−3)		→ 0 (x→∞)
	ex