matematykaszkolna.pl
Zespolone Basiek: Zespolone emotka Może macie jakieś zadanka z liczb zespolonych (nie jakieś super − super trudne), których możnaby użyć w celu powtórki? Pozdrawiam, B.
16 sty 22:33
Saizou : Wyznacz pierwiastki 8 stopnia z jedynki, kochana okularnico emotka
16 sty 22:34
Basiek: Cześć, Saizou. Dzięki, zadanko uświadamia mi, jak wiele nie pamiętam.
16 sty 22:37
Saizou : Witam Cię Basiu, zgadnij na jakim kierunku wylądowałem
16 sty 22:38
Saizou : albo jeszcze takie coś: obliczyć cos(6x) i sin(6x), oczywiście korzystając z liczb zespolonych
16 sty 22:40
Saizou : no i jeszcze coś takiego obliczyć zn−(z→)n gdzie z→ to sprzężenie z
16 sty 22:42
Basiek: Matematykę?
16 sty 22:43
Saizou : hihi tak
16 sty 22:43
Basiek: Stooooooop.
16 sty 22:43
Saizou : ok... poczekam na pierwiastki 8−st z 1
16 sty 22:45
Basiek: Możesz się dziś nie doczekać
16 sty 22:48
Saizou : po prosty rozwiązujemy z6−1=0
16 sty 22:50
5-latek: Na razie wpisz do wolframa i napisz Saozou a jutro sobie policzysz emotka
16 sty 22:50
Basiek: Nie oszukujemy, to nieładnie!
16 sty 22:51
Basiek: Podstawowy problem: trzeba odnaleźć kalkulator.
16 sty 22:52
Saizou : ale po co kalkulator
16 sty 22:56
Basiek: Ale się zrobiłeś czepialski... emotka
16 sty 22:59
Saizou : studia wymusiły ode mnie nieużywanie kalkulatora
16 sty 23:01
5-latek: W koncu przyszły matematyk emotka
16 sty 23:01
Saizou : my tu gady−gadu a pierwiastki same się nie policzą
16 sty 23:05
Basiek:
 √2 √2 √2 √2 √2 √2 
8√1={1,
+
i, i, −
+
i, −1, −
−
i, −i,
 2 2 2 2 2 2 
 √2 √2 
−
−
i}
 2 2 
16 sty 23:06
Saizou : oł kej a obliczenia
16 sty 23:11
Basiek: Nie mówisz serio...
16 sty 23:12
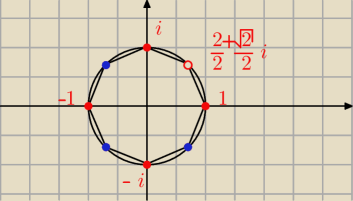
Saizou : rysunek jest dobrze
16 sty 23:15
Saizou : zapomniałem wpisać na rysunku pierwiastka
16 sty 23:21
Basiek: Wiem, wiem. Sprawdziłam sobie to tym samym trikiem, żeby nie było wstydu. http://prntscr.com/5tcm3m (Żeby nie było, że oszukiwałam, jeśli jesteś estetą, to nie patrz, nie zamierzałam pierwotnie chwalić się tym zapisem.)
16 sty 23:21
Basiek: Aaa to cos(6x) i sin(6x), to kompletnie nie wiem, jak mam obliczyć. Czy to po prostu nie będzie:
 e6xi+e−6xi 
cos(6x)=
 2 
 e6xi−e−6xi 
sin(6x)=
 2i 
16 sty 23:29
Saizou : bo nie sprecyzowałem treści rozpisz cos6x i sin6x względem sinx i cosx
16 sty 23:30
Basiek: No tego w zeszycie nie znajdę. Książko, gdzie jesteś?
16 sty 23:32
Saizou : podpowiem że to z pana Moivre
16 sty 23:34
Basiek: Do tego już doszłam, ale serio oczekujesz, że obliczę sobie radośnie ze wzoru dwumianowego cos(6x)?
16 sty 23:36
Basiek: Powtórzę: 6x
16 sty 23:36
Saizou : 6x to mało tym bardziej że jak raz to zrobisz to masz od razu sin6x i cos6x
16 sty 23:37
Basiek: Połowa z tego, co? 3x jak znalazł. Zlituj się, potrzebuję jeszcze tej nocy z godzinkę spędzić nad całkami.
16 sty 23:38
Basiek: No dooobra! Robię szóstkę. Uwaga, to potrwa.
16 sty 23:38
Saizou : weź zrób sobie trójkąt Pascala i masz już współczynniki
16 sty 23:39
Basiek: Hm, no tak. Trójkąt Pascala. To też sobie przypomnę. TABULA RASA to ja. Dziś się utożsamiam. Kolos w środę. Ech. Zaczynam liczyć!
16 sty 23:41
Saizou : trzymam kciuki
16 sty 23:43
Basiek: http://prntscr.com/5td40z Kciuki Ci zdrętwieją... emotka
16 sty 23:55
Saizou : tylko że jak piszesz np. z=(cosx+isinx)6=cos6x+isin6x to zapisz Re(z)=cos6x=.... Im(z)=sin6x=.... a tak jest dobrze
16 sty 23:58
Basiek: A to ostatnie jest straszne i ja wiem tylko, że zn− (−z−)n= rn[(cosnφ+isinnφ)−(cos(−nφ)+isin(−nφ)]=... ?
17 sty 00:02
Saizou : eh... tam miał być zn+(z−)n
17 sty 00:06
Basiek: Nie wyjdzie to w jakiś super super sposób 2Re(z)=2x?
17 sty 00:08
Mila: Nie wiem jaki to ma być poziom, ale podaję praktyczne porady. http://cmf.p.lodz.pl/~gkusztelak/liczby_zesp_odp.pdf http://www.fuw.edu.pl/~wkaminsk/zespolone.pdf
17 sty 00:10
Saizou : skorzystaj z tego co napisałaś rn[(cosnφ+isinnφ)+(cos(−nφ)+isin(−nφ)]
17 sty 00:10
Saizou : nie wiem czy tam jest to ale
 2π 2π 
ωn=ωn−1(cos
+isin
)
 n n 
jest to wzór na n−ty pierwiastek z jedynki (wystarczy znać jakikolwiek pierwiastek i można sobie wszystko obliczyć )
17 sty 00:13
Basiek: Milu, obawiam się, że wysoki. Mimo, że raczej nie spodziewam się "udowodnij, że..." Dzięki za materiały. Na pewno przeglądnę. Saizou, czy ja mogę dodawać sin do sin i cos do cos? Przy mnożeniu był taki wzór, ale dodawanie...?
17 sty 00:14
Saizou : możesz, przecież tu działają takie same działania jak w R
17 sty 00:16
Basiek: Mój matematyk by Cię za takie sformułowanie wyśmiał i słownie zlinczował. Ała.
17 sty 00:17
Saizou : to jest pewien skrót myślowy
17 sty 00:18
Basiek: Serio jest takie twierdzenie, które pozwala to dodać? Ty chcesz, żebym to dodała?
17 sty 00:18
Saizou : bo liczby zespolone wprowadza się tak: w zbiorze R2 par liczb rzeczywistych określamy działania (a,b)+(c,d)=(a+c,b+d) (a,b)•(c,d)=(ac−bd,bc−ad) no i to tworzy ciało liczb zespolonych ale z postaci pary mozna przejśc do postaci kanonicznej
17 sty 00:21
Saizou : tak na prawdę robisz to samo co dla pary w R2
17 sty 00:22
Basiek: Dobra, po małych konsultacjach już wiem! Uwaga, odpowiadam: =rn[cosnφ+isinnφ+cosnφ−isinnφ]=rn*2cos(nφ) To ze względu na parzystość cosinusa i nieparzystość sinusa.
17 sty 00:23
Basiek: Sorry, ale to było zbyt oczywiste. Dawno nie widziałam oczywistych zadań i wtedy jakoś tak wydaje mi się, że to podstęp iiii w ogóle jest źle.
17 sty 00:24
Saizou : no i jest ok to co udowodnij wzory de Moivre ?
17 sty 00:25
Basiek: W udowadnianie bym nie wchodziła, muszę na środę ogarnąć zespolone, algebrę i analizę.
17 sty 00:26
Saizou : ja dzisiaj po kole z algebry, jeszcze logika i analiza
17 sty 00:27
Basiek: Łączę się w bólu. Ja staram sie jednym okiem zespolone, drugim całki, gdzieś tam z boku ekstrema... Boli mnie życie. Ale wiem, co czujesz!
17 sty 00:28
Saizou : mnie z analizy brakuje 9 ptk żeby zaliczyć ćwiczenia, wiec luz, no i jeszcze logika ćw ale tu musze zaliczyć koło, a potem uczyć się do sesji
17 sty 00:29
Godzio: Stare dobre czasy ... analiza, algebra
17 sty 00:30
Basiek: Mnie też 9. Za kolosa jest 28. Ale to są naprawdę trudne zadanka. Serio serio serio. Mogę Ci pokazać jakieś. Mniej, niż 30%, a taki stres...
17 sty 00:31
Saizou : zapodaj, to ja mam na 50 Godzio podzielasz zdanie PW https://matematykaszkolna.pl/forum/274324.html
17 sty 00:33
Godzio: Czytałem to zadanie, ale nie mam pojęcia jak to się robiło, to było 3 lata temu, a nigdy więcej z tego nie korzystałem
17 sty 00:34
Saizou : no cóż.... zapytam się może w poniedziałek profesora
17 sty 00:36
Godzio: Zaraz pomyślę jeszcze.
17 sty 00:38
Saizou : ale ja chyba mykam, jutro trzeba wstać i sprzątać................eh... ale dziękuję za zainteresowanie
17 sty 00:38
Basiek: To np. z pierwszego (podobno sporo prostszego) kolokwium: http://prntscr.com/5tdnui Podobało mi się jeszcze jedno: http://prntscr.com/5tdou2 Sorry, ale nie chciałabym, żeby mnie ktoś zdybał. Wiadomo, że kolosy i egzaminy z poprzednich lat krążą... screenami trudniej znaleźć.
17 sty 00:39
Basiek: PS Jakby ktoś dla zabawy sobie robił i chciał się podzielić rozwiązaniem, to jestem całym serduszkiem za. Saizou, dzięki, dobranoc. emotka
17 sty 00:40
Saizou : skończyłem to czytać na wyrażaniu dany jest homomorfizm i pół alfabetu
17 sty 00:41
Basiek: Takie kolosy <3
17 sty 00:42
Godzio: PW ma rację, tak powinno się zrobić emotka
17 sty 00:45