analityczna kyrtap: Znaleźć równanie krawędziowe prostej przechodzącej przez punkty (−3,4,1), B = (0,2,1). Jak się do tego zabrać?

AS: Zajrzeć do podręcznika (zeszytu) i poszukać podstawowego wzoru a nie pytać się o elementarz.

Mila: Najpierw napisz równanie parametryczne prostej.

Mila: albo kierunkowe.

Metis: Mila możesz zerknąć ? 274100

kyrtap: o jaki elementarz , czytałem te wzory ale za cholerę nie wiem jak sobie tu poradzić znam wzory i wiem jak doprowadzić do postaci parametrycznej krawędziową postać też znam bo to jest układ równań dwóch równań ogólnych płaszczyznywowe

kyrtap: mógłby ktoś pomóc z tym i zobrazować to czytam podręcznik skoczylasa i dalej nie wiem jak to zrobić

AS: A = (3,−4,1) , B = (0,2,1) Równanie krawędziowe

x − xo		y − yo		z − zo
	=		=
a		b		c

gdzie [a,b,c] jest wektorem równoległym do prostej a = 0 − 3 = −3 , b = 2 + 4 = 6 , c = 1 − 1 = 0 , w = [−3,6,0] Równanie krawędziowe

x − 3		y + 4		z − 1
	=		=
−3		6		0

kyrtap: AS mówisz do mnie o elementarzu a sam mylisz pojęcia gdzie sens gdzie logika ?

Mila: A(−3,4,1), B = (0,2,1). 1) wektor AB AB^→=[3,−2,0] wektor kierunkowy prostej Równanie parametryczne : x=−3+3t y=4−2t z=1+0t, t∊R 2) Równanie krawędziowe: x=−3+3t y=4−2t z=1 2t=4−y

	1
t=2−		y podstawiam do I równania
	2

	1		3
x=−3+3*(2−		y)⇔x=−3+6−		y
	2		2

	3
x=3−		y
	2

	3
x+		y−3=0 /*2
	2

stąd: 2x+3y−6=0 dołączamy drugie równanie z−1=0

kyrtap: czyli równanie krawędziowe będzie miało postać

⎧	2x + 3y − 6 = 0
⎩	z − 1 = 0

kyrtap:

AS: O co chodzi? Pomyliłem współrzędne punktu A. Miało być A = (−3,4,1) , B = (0,2,1) Równanie krawędziowe

x + 3		y − 4		z − 1
	=		=
3		−2		0

Errare humanum est − tak mawiali starożytni.

kyrtap: z tego co czytam w elementarzu to co zapisałeś jest postacią kierunkową prostej a nie krawędziową

kyrtap: Milu czyli to jest postać krawędziowa tak? ta co podałem?

Mila: Postać krawędziowa 18:37

Mila: AS podał postać kierunkową prostej. Masz w takim razie 3 równania tej samej prostej.

kyrtap: dzięki ślicznie teraz czekamy Milu na Graya odnośnie tamtego zadania

AS: Proponuję takie rozwiązanie mam dane dwa punkty,które wyznaczają prostą, która jest wspólną krawędzią dwóch płaszczyzn. Obieram trzeci punkt nie należący do tej krawędzi np. C(1,3,4) Równanie płaszczyzny przechodzącej przez punkty A,B i C ma postać 6*x + 9*y − 5*z − 13 = 0 Dla innego punktu np. D(2,5,−4) mamy płaszczyznę 10*x + 15*y + 13*z − 43 = 0 Wtedy równaniem krawędziowym może być układ równań 6*x + 9*y − 5*z − 13 = 0 10*x + 15*y + 13*z − 43 = 0

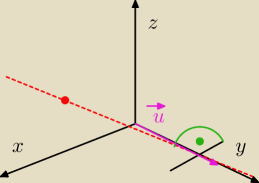
kyrtap: proszę o sprawdzenie kolejnego zadania Znaleźć równanie parametryczne i krawędziowe prostej przechodzącej przez punkt P = (3,−1,2) i przecinającej prostopadle oś oy znajduję sobie wektor u^→ = [0,5,0] wiem też że aby znaleźć równanie w postaci parametrycznej potrzebuję wektora równoległego do prostej z warunku u^→ ◯ V^→ = 0 gdzie V^→ = [a,b,c] znajduje równanie jakie musi spełniać wektor V^→ aby był równoległy do prostej (czerwonej) [0,5,0] ◯ [a,b,c] = 0 5b = 0 stąd mój wektor równoległy do prostej ma postać np: V^→ = [3,0,1] i teraz mogę zapisać równanie parametryczne:

⎧	3 + 3t
⎨	−1 + 0t	dobrze
⎩	2 + t

kyrtap: ?

kyrtap: ?

kyrtap: ?

Gray: Dobrze.

kyrtap:

Mila: Współrzędne rzutu prostopadłego punktu P na oś Oy to P'=(0,−1,0) PP'^→=[−3,0,−2] to jest wektor równoległy do szukanej prostej k^→=[−3,0,−2] albo moze być [3,0,2] wektor kierunkowy prostej x=3+3t y=−1 z=2+2t, t∊R

Gray: Jasne; moja pomyłka − nie zauważyłem braku tej 2. Ta prosta, którą wyznaczyłeś jest prostopadła do osi Oy i przechodzi przez punkt (−3,−1,2), ale nie przecina osi Oy.

Mila: Witaj Gray. Na rowerku byłeś, czy u Ciebie pada. U mnie pogoda rowerowa. Śmieszna zima.

Gray: Cześć Mila. Nie, nie byłem na rowerku. Pogoda faktycznie rowerowa, ale z czasem kiepsko.