analityczna kyrtap: Nie rozumiem przykładu: Znaleźć równanie parametryczne płaszczyzny przechodzącej przez punkt A = (−2,5,4) oraz prostopadłej do osi OY jeżeli płaszczyzna prostopadła do osi OY to wniosek z tego że jej wektor normalny n^→ =(0,1,0) zgodnie z definicją równania parametrycznego muszę mieć dwa wektory rozpinające płaszczyznę znajduje je są to np: u^→= (0,0,1) V^→ = (−1,00) potrzebuje również wektora wodzącego(wektor który zaczyna się w początku układu współrzędnych) jak go znaleźć bo to nie będzie chyba OA^→ przyjmując że O= (0,0,0)

kyrtap: v^→ =(−1,0,0)

kyrtap:

kyrtap:

kyrtap:

kyrtap: i jeszcze jeno pokazać że równania parametryczne:

⎧	x = 3− t + 2s
⎨	y= −1 +t	,
⎩	z = 2+ t −3s

	⎧	x = 4 + 3t+3s
	⎨	y = t −s
	⎩	z = −2t −4s

jeżeli przedstawię te równania w postaci ogólnej i współczynniki A B C D będą te same to pokazałem że równania te przedstawiają tę samą płaszczyznę?

kyrtap:

Mila: Jeżeli [A,B,C ] || [A'B'C'] to płaszczyzny są równoległe. Jeżeli mają jeden punkt wspólny to pokrywaja się. Jeżeli po przekształceniach otrzymujesz to samo równanie to masz tę samą płaszczyznę. 1) π: x+y+z−10=0 2x+2y+2z−20=0 ta sama plaszczyzna =================== 2) Q: x+y+z−5=0 Q||π

kyrtap: Mila a jak z zadaniem pierwszym

kyrtap: Jutro będziesz?

kyrtap: Nadal czekam

kyrtap:

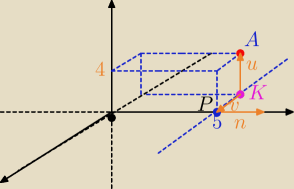
Mila: A=(−2,5,4) Równanie ogólne płaszczyzny prostopadłej do osi OY n^→=[0,1,0] wektor normalny płaszczyzny π: 0*(x+2)+1*(y−5)+0*(z−4)=0⇔ π: y=5 ( w takim razie z , x∊R dowolne ?) ================= Równanie parametryczne : u||π , u^→=[0,0,4] || [0,0,1] v^→||π, v^→=[2,0,0]|| [1,0,0] P=(0,5,0) x=0+0s+1t y=5+0s+0t z=0+1s+0t, t, s∊R ⇔ x=t y=5 z=s

kyrtap: Mila piękne dzięki jutro raniutko będę rozkminiał to

kyrtap: nie czaję za bardzo tej analitycznej

kyrtap: Mila to jest ta cała płaszczyzna

kyrtap: tylko taka powyginana

kyrtap: dobra ta już mącę sobie w głowie

kyrtap: Mila ? pytanko jeszcze tego zadania z pokazaniem ? sory że tak dużo pytam

Mila: ?

kyrtap: Jeżeli [A,B,C ] || [A'B'C'] to płaszczyzny są równoległe.( to jakoś zrozumiem) Jeżeli mają jeden punkt wspólny to pokrywaja się.( mogłabyś to zobrazować na rysunku) Jeżeli po przekształceniach otrzymujesz to samo równanie to masz tę samą płaszczyznę.

Mila: Jeżeli [A,B,C ] || [A'B'C'] i mają jeden punkt wspólny, to pokrywają się. Niezbyt precyzyjnie tam się wyraziłam.22:03 Późna pora. Wyjasniam. Podobnie jak z prostymi. k: 2x+y−5=0 m: 4x+2y−10=0 [2,1] || [4,2] Możesz drugie równanie podzielić przez 2 i masz to samo równanie: 2x+y−5=0 proste pokrywaja się. Albo weźmiesz P(1,3)∊k sprawdzam 4*1+2*3−10=4+6−10=0 proste rónoległe pokrywają się. Ale w przypadku n: 4x+2x−20=0 i [2,1] || [4,2] 4*1+2*3−20≠0⇔k||n i proste nie pokrywaja się.

kyrtap: Czyli warunkiem aby dwie płaszczyzny lub dwie proste pokrywały się muszą ich wektory być równoległe w przypadku płaszczyzn wektory normalne oraz ich równania ogólne były tej samej postaci dobrze kumam

Mila: Dobrze.

Mila: Takie same równania po doprowadzeniu do najprostszej postaci.

kyrtap: Śliczne dzięki, rozwiałaś wszelkie moje wątpliwości, ty Milu jakoś możesz to wszystko ładnie zobrazować

Mila: Dobranoc.

kyrtap: Dobranoc jeszcze raz dziękuje

kyrtap: Mila wniosek z tego taki że jest błąd w zadaniu bo ani te dwie płaszczyzny nie mają równoległych wektorów normalnych ani nie ich równania ogólne nie są takie same

Mila: Które płaszczyzny, napisz .

kyrtap: zaraz

kyrtap: pokażę może rozwiązanie

kyrtap:

	⎧	x = 3 − t +2s
π1 :	⎨	y = −1 +t
	⎩	z = 2 + t − 3s

BA^→ = [−1,1,1] CA^→ = [2,0,−3] A = (3,−1,2) n₁ → = BA^→ x CA^→ = −3i +2j − 2k − 3j = −3i − j − 2k ⇒ n^→ = [−3,−1,−2] π₁ : −3(x−3) + (−1)(y+1) + (−2)(x−2) = 0 −3x + 9 − y − 1 − 2z +4 =0 −3x − y − 2z + 12 = 0

	⎧	x = 4 + 3t + 3s
π2 :	⎨	y = t −s
	⎩	z = −2t − 4s

ED^→ = [3,1,−2] , FD^→ = [3,−1,−4] D = (4,0,0) ED^→ x FD^→ = −4i − 6j − 3k − 3k − 2i + 12j = −6i + 6j − 6k ⇒ n₂^→ = [−6,6,−6] n₁^→ i n₂ ^→ nie są równoległe do siebie π₂ : −6(x−4) + 6y − 6 z = 0 −6x + 6y − 6z + 24 = 0 stąd płaszczyzny nie przedstawiają tej samej płaszczyzny

kyrtap: dobrze?

Mila: −6x + 6y − 6z + 24 = 0 /:(−6) x−y+z−4=0 n₁^→=[−3,−1,−2] n₂^→=[1,−1,1] wektory nie są równoległe. Poprosimy Graya'a o konsultację. Byc może ,źle to pamiętam. Zadanie z 21:03.

kyrtap: mi się wydaję że błąd w zadaniu jak ja ogarnę analityczną strasznie dziwna jest

Gray: Cześć. Jeżeli chodzi o zadania z 21:03 to to są różne płaszczyzny (nie są również równoległe).

kyrtap: Gray https://matematykaszkolna.pl/forum/274302.html