Trygonometria Jednorożec michał:

	3π		7π		5π
Liczba sin		*cos		* tg		jest równa :
	4		3		3

	4		1
Najmniejszą wartością funkcji f(x)=		cos2(2x+1)−		x∊R jest liczba
	9		3

Proszę o pomoc z wytłumaczeniem . W przypadku drugiego zadania chciałbym poprosić o wyjaśnienie dodatkowo z największą wartością .

Mila: 1) https://matematykaszkolna.pl/strona/397.html i wzory redukcyjne

3π		1
	=π−
4		4

	3π		1		π		√2
sin(		)=sin(π−		π) =sin		=
	4		4		4		2

Dalej sam, jeśli chcesz czegoś się nauczyć. 2)

	4
0≤cos2(2x+1)≤1 /*		⇔
	9

	4		4		1
0≤		cos2(2x+1)≤		/−		⇔
	9		9		3

	1		4		1		1
−		≤		cos2(2x+1)−		≤
	3		9		3		9

	1		1
Zwf=<−		,
	3		9

Jednorożec michał: a w przypadku gdy jest zadanie :

	1
Największą wartością funkcji f(x)=		, x∊<pi/4 ; pi/2> jest liczba :
	tg2 x + 1

1≤tg² x / +1 2≤tg² x + 1

1		1
	≤
2		tg2 x +1

Najwiekszą wartoscią funkcji jest liczba 1/2 ? Dobrze ?

Mila: Tak.Dobrze.

	π		π
x∊<		,		)
	4		2

	π		π		π
W przedziale <		,		) tg2x jest funkcją rosnącą⇔ma najmniejszą wartość dla x=
	4		2		4

	π
tg2(		)=12=1
	4

	1		1
Największa wartość f(x)w podanym przedziale to		=
	1+1		2

II sposób

1		1		1
	=		=		=cos2x
tg2x+1		sin2x   +1 cos2x		sin2x+cos2x   cos2x

	π		π
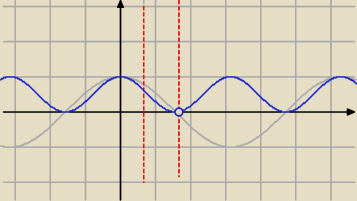
f(x)=cos2 jest funkcja malejącą w przedziale <		,		)
	4		2

	π		√2		2		1
f(		)=(		)2=		=		− najwieksza wartość f(x) w przedziale
	4		2		4		2

	π		π
<		,		)
	4		2