pochodna
matematyk: czy poprawnie obliczyłem pochodną?
| | 2x | | 1 | | 2x | | 2 | |
(arcsin |
| )' = |
| *( |
| )' = ....= − |
| |
| | 1+x2 | | | | 1+x2 | | 1+x2 | |
5 sty 22:41
matematyk: 
5 sty 22:47
matematyk: 
5 sty 22:57
matematyk: proszę o spr
5 sty 23:01
matematyk: 
?
5 sty 23:24
matematyk: nie wiem czy mam dobrze

5 sty 23:24
matematyk: rozwinę swój zapis

5 sty 23:34
niechciany: źle masz.
5 sty 23:47
matematyk: | | 4x2 | | (2x)'(1+x2)−2x(1+x2)' | |
U{1}{√1 − |
| |
| = |
| | (1+x2)2 | | (1+x2)2 | |
| | 1 | | 2(1+x2)−2x* 2x | |
|
| |
| = |
| | | | (1+x2)2 | |
| 1 | | 2+2x2 − 4x2 | |
| * |
| = |
| | (1+x2)2 | |
| 1 | | 2−2x2 | | x2+1 | | 2(1−x2) | |
| * |
| = |
| * |
| = |
| | (1+x2)2 | | x2−1 | | (1+x2)2 | |
| (x2+1)(−2)(x2−1) | | −2 | |
| = |
| |
| (x2−1)(1+x2) | | 1+x2 | |
5 sty 23:47
matematyk: gdzie dokładnie
5 sty 23:47
niechciany: | | 2 * sgn(x2 − 1) | |
= − |
| |
| | x2 + 1 | |
5 sty 23:47
5 sty 23:48
niechciany: √(x2 − 1)2 = |x2 − 1| − tu masz błąd.
5 sty 23:49
matematyk: co


5 sty 23:49
5 sty 23:51
matematyk: no dobra bo tak w ogóle mam tożsamość do uzasadnienia i za cholerę mi nie wychodzi mianowicie
| | 2x | |
arcsin |
| = 2arctgx dla x ∊(−1,1) |
| | 1+x2 | |
5 sty 23:57
matematyk: 
6 sty 00:00
niechciany: | | 2x | |
Zdefiniuj funkcję : f(x) = arcsin( |
| ) − 2arctgx dla x ∊ (−1 , 1) |
| | 1 + x2 | |
Zauważmy, ze
| | −2 sgn(x2 − 1) | | 2 | |
f'(x) = |
| − |
| = |
| | x2 + 1 | | x2 + 1 | |
| | −2 * (−1) | | 2 | |
= |
| − |
| = 0 |
| | x2 + 1 | | x2 + 1 | |
Skoro pochodna jest równa zero to funkcja f jest funkcją stałą. Wystarczy policzyć jej wartość
w jakimś "ładnym punkcie"
f(0) = arcsin0 + arctg0 = 0 zatem :
| | 2x | |
f(x) = 0 = arcsin( |
| ) − 2arctgx |
| | 1 + x2 | |
skąd
| | 2x | |
arcsin( |
| ) = 2arctgx dla x ∊ (−1 , 1) |
| | 1 + x2 | |
6 sty 00:01
matematyk: czemu sgn(x
2−1) zamieniasz na (−1)

6 sty 00:05
niechciany: a co to jest sgn ?
6 sty 00:06
matematyk:
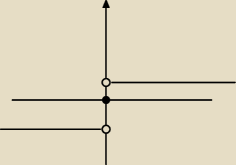
6 sty 00:07
niechciany: masz x ∊ (−1 , 1). Ile wynosi sgn(x
2 − 1) ?

6 sty 00:08
matematyk: no (−1)

6 sty 00:09
niechciany:
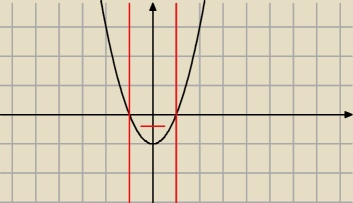
6 sty 00:10
matematyk: dziękuje
6 sty 00:13


 ?
?









