zadanie
Blue: W trójkącie prostokątnym ABC wysokość CD poprowadzona z wierzchołka kata prostego c podzieliła
przeciwprostokątną na odcinki AD i BD. Wykaż, że |CD|=
√|AD|*|BD|
Czyli muszę wykazać, że te odcinki tworzą c. geometryczny

Ale jak to zrobić?
4 sty 19:03
Kacper:
Podobieństwo trójkątów.
To bardzo łatwe zadanie.
4 sty 19:07
Eta:
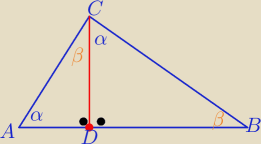
Trójkąty ADC i DBC są podobne z cechy (kkk)
| |CD| | | |DB| | |
| = |
| ⇒ ....... teza |
| |AD| | | |CD| | |
4 sty 19:08
Blue: Dzięki Eta, rzeczywiście proste zadanie

4 sty 19:13
Eta:
Zadanie z gimnazjum

4 sty 19:17
hejka:
A Ty Blue po takim tu wielomiesięcznym treningu też komuś pomogłaś?, bo widzę, że wciąż
ciągle nie jesteś samodzielna i oczekujesz wytarcia przez nianię swojego noska?
4 sty 19:19
Kacper:
I okazało się prawdą co mówiła
Eta i
Mila 
4 sty 19:33
Blue: 
4 sty 19:38
Blue: no bo ja po prostu nie umiem planimetrii i tyle

4 sty 19:38
hejka:
Nie odpowiedziałaś na pytanie. Czy Ty Blue komuś tu pomogłaś?
4 sty 19:46
Blue: Celowo. Nie miałam zamiaru odpowiadać na głupie komentarze. Rzadko pomagam innym, chociaż chyba
kilka razy się zdarzyło. A co Ciebie to tak interesuje?

4 sty 19:54
Eta:
@
Blue planimetria dla treningu
 zad.1
zad.1 wykaż,że w trójkącie prostokątnym o przyprostokątnych
a i
b
suma długości średnic okręgu wpisanego i okręgu opisanego na tym trójkącie
jestdwa razy większa od średniej artymetycznej długości przyprostokątnych.
zad.2wykaż,że jeżeli przekątna trapezu równoramiennego jest dwusieczną kąta ostrego
trapezu i tworzy z drugim ramieniem kąt prosty,to kąt ostry trapezu ma miarę
60o
zad.3W trójkącie ABC środkowa poprowadzona z wierzchołka C przecina bok AB
w punkcie D, zaś półprosta DE jest dwusieczną kąta BDC.
Wykaż,że jeżeli DE⊥BC , to trójkąt ABC jest prostokątny.
Powodzenia

4 sty 20:28
Eta:
Gdzie jest
Blue? wystraszyła się?

4 sty 21:02
bezendu:
Pewnie tak

4 sty 21:04
Eta:
@
bezendu nie rozwiązuj

4 sty 21:08
bezendu:
Eta gdybym jeszcze umiał

4 sty 21:36
Blue: Eta, dziękuję

Zaraz się biorę za te zadanka

5 sty 16:58
Blue: Chociaż, skoro bezendu mówi, że nie umie, to jestem przekonana na 99,(9) %, że ich nie
rozwiążę, ale zawsze warto spróbować

5 sty 16:59
Eta:
Musisz rozwiązać i na pewno dasz radę ( nie są trudne

5 sty 17:04
Blue: Zrobiłam te dwa pierwsze, ale z trzecim się męczę. Zaraz wrzucę skany...
5 sty 17:28
Blue:
Ej

Zrobiłam to trzecie też, ale nie wiem, czy dobrze

5 sty 17:39
Eta:
No i bardzo dobrze

( pokaż skany,to sprawdzę
5 sty 17:41
kyrtap: 
5 sty 17:45
Blue: Poczekajcie chwilkę, mój skaner zamula

Zaraz będą...

5 sty 17:46
kyrtap: spoko poczekam

Eta też poczeka

5 sty 17:46
Eta:
Ja na razie idę piec pizzę

5 sty 17:47
kyrtap: pizza powiadasz a z czym?
5 sty 17:48
Eta:
Z żółtym serem

5 sty 17:49
kyrtap: Margherita powiadasz smacznego w takim razie

5 sty 17:50
5 sty 17:54
Blue: Nie zapomnij pokroić kawałków w kształcie delty^^
5 sty 17:54
Blue: Czekam na opinię

5 sty 18:20
Eta:
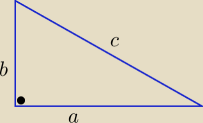 Blue
Blue
zad1

ale nakombinowałaś
rozwiązanie w
2minuty
W tablicach masz wzory( jak nie pamiętasz)
to 2R+2r= c+a+b−c = a+b
i odpowiedź .....
5 sty 22:22
Eta:
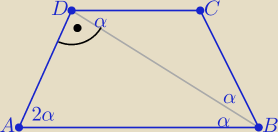
Zad2..... no ....zaliczone
ale... staraj się elegancko, przejrzyście z oznaczeniami sporządzać rysunki
( nie rysuj
bohomazów !
Mogłaś też tak opisać na podstawie ładnego rys.
|<ADB|=90
o −− z treści zadania, BD jest dwusieczną kąta ABC
to w trójkącie prostokątnym ABD : 2α+α=90
o ⇒ α= 30
o
to kąty ostre trapezu mają miarę 2α= 60
o
5 sty 22:38
Eta: 3/ ok
5 sty 22:40
Mila:
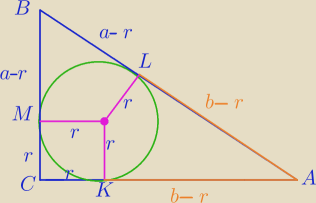
ΔABC− Δprostokatny
r− promień okręgu wpisanego w ΔABC
R− promień okręgu opisanego na ΔABC
|AB|=2R
|AC|=b
|BC|=a
Punkty styczności okręgu z ramieniem są jednakowo odległe od wierzchołka kąta.
a−r+b−r=2R⇔
a+b=2r+2R⇔
| | a+b | |
2* |
| =2r+2R gdzie 2r,2R− średnice... |
| | 2 | |
5 sty 22:43
Eta:
Mila ja nie zabieram Ci
Blue 
( bo nie lubię otwierać tych linków ze skanami

5 sty 23:48
5 sty 23:52
Blue: Ja czasem chodzę okrężnymi ścieżkami ^^ Tak już mam

6 sty 10:21
 Ale jak to zrobić?
Ale jak to zrobić?
 Trójkąty ADC i DBC są podobne z cechy (kkk)
Trójkąty ADC i DBC są podobne z cechy (kkk)






 zad.1 wykaż,że w trójkącie prostokątnym o przyprostokątnych a i b
suma długości średnic okręgu wpisanego i okręgu opisanego na tym trójkącie
jestdwa razy większa od średniej artymetycznej długości przyprostokątnych.
zad.2wykaż,że jeżeli przekątna trapezu równoramiennego jest dwusieczną kąta ostrego
trapezu i tworzy z drugim ramieniem kąt prosty,to kąt ostry trapezu ma miarę 60o
zad.3W trójkącie ABC środkowa poprowadzona z wierzchołka C przecina bok AB
w punkcie D, zaś półprosta DE jest dwusieczną kąta BDC.
Wykaż,że jeżeli DE⊥BC , to trójkąt ABC jest prostokątny.
Powodzenia
zad.1 wykaż,że w trójkącie prostokątnym o przyprostokątnych a i b
suma długości średnic okręgu wpisanego i okręgu opisanego na tym trójkącie
jestdwa razy większa od średniej artymetycznej długości przyprostokątnych.
zad.2wykaż,że jeżeli przekątna trapezu równoramiennego jest dwusieczną kąta ostrego
trapezu i tworzy z drugim ramieniem kąt prosty,to kąt ostry trapezu ma miarę 60o
zad.3W trójkącie ABC środkowa poprowadzona z wierzchołka C przecina bok AB
w punkcie D, zaś półprosta DE jest dwusieczną kąta BDC.
Wykaż,że jeżeli DE⊥BC , to trójkąt ABC jest prostokątny.
Powodzenia 




 Zaraz się biorę za te zadanka
Zaraz się biorę za te zadanka


 Zrobiłam to trzecie też, ale nie wiem, czy dobrze
Zrobiłam to trzecie też, ale nie wiem, czy dobrze 
 ( pokaż skany,to sprawdzę
( pokaż skany,to sprawdzę

 Zaraz będą...
Zaraz będą... 
 Eta też poczeka
Eta też poczeka 




 Blue
zad1
Blue
zad1  ale nakombinowałaś
rozwiązanie w 2minuty
W tablicach masz wzory( jak nie pamiętasz)
ale nakombinowałaś
rozwiązanie w 2minuty
W tablicach masz wzory( jak nie pamiętasz)
 Zad2..... no ....zaliczone
ale... staraj się elegancko, przejrzyście z oznaczeniami sporządzać rysunki
( nie rysuj bohomazów !
Mogłaś też tak opisać na podstawie ładnego rys.
|<ADB|=90o −− z treści zadania, BD jest dwusieczną kąta ABC
to w trójkącie prostokątnym ABD : 2α+α=90o ⇒ α= 30o
to kąty ostre trapezu mają miarę 2α= 60o
Zad2..... no ....zaliczone
ale... staraj się elegancko, przejrzyście z oznaczeniami sporządzać rysunki
( nie rysuj bohomazów !
Mogłaś też tak opisać na podstawie ładnego rys.
|<ADB|=90o −− z treści zadania, BD jest dwusieczną kąta ABC
to w trójkącie prostokątnym ABD : 2α+α=90o ⇒ α= 30o
to kąty ostre trapezu mają miarę 2α= 60o
 ΔABC− Δprostokatny
r− promień okręgu wpisanego w ΔABC
R− promień okręgu opisanego na ΔABC
|AB|=2R
|AC|=b
|BC|=a
Punkty styczności okręgu z ramieniem są jednakowo odległe od wierzchołka kąta.
a−r+b−r=2R⇔
a+b=2r+2R⇔
ΔABC− Δprostokatny
r− promień okręgu wpisanego w ΔABC
R− promień okręgu opisanego na ΔABC
|AB|=2R
|AC|=b
|BC|=a
Punkty styczności okręgu z ramieniem są jednakowo odległe od wierzchołka kąta.
a−r+b−r=2R⇔
a+b=2r+2R⇔
 ( bo nie lubię otwierać tych linków ze skanami
( bo nie lubię otwierać tych linków ze skanami 
