ciągi/geometria pikolo: Bardzo proszę o pomoc w tych dwóch zadaniach:

	2+4+6+...+2n
1.Dany jest ciąg an o wyrazie ogólnym an=
	n+2 2

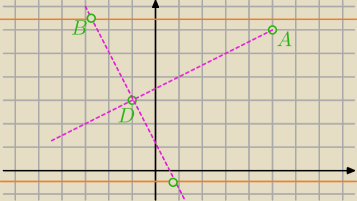
−wykaż z definicji że ciąg jest rosnący −ile wyrazów tego ciągu jest mniejszych od 1.99? 2.Punkty A(5,6) i D(−1,3) są końcami wysokości trójkąta równobocznego ABC. Wyznacz współrzędne B i C oraz równanie okręgu wpisanego w trójkąt ABC

===: 1) 2+4+6+...+2n=(n+1)n

	n+2 2		n!(n+1)(n+2)		(n+1)(n+2)
		=		=
			2!n!		2

zatem:

	2n(n+1)		2n
an=		=
	(n+1)(n+2)		n+2

... dalej już dla Ciebie −

pikolo: tak, dam sobie rade. A zadanie nr 2?

daras: https://matematykaszkolna.pl/strona/542.html

pikolo: A jak sobie poradzić ze współrzędnymi punktów C i B?

===: ... nie przesadzaj ... wszak wiesz, że to trójkąt równonoczny

pikolo: to chociaż pomóż mi w kolejności liczenia: 1.długość odcinka AD 2.wyliczenie z tego długości boku 3.mogę wyznaczyć współczynnik BC tylko nie wiem jaki uklad równań ułożyć by obliczyć wsp.tych punktów.

===: ... jak zawsze w matematyce ... ścieżek jest kilka Wybór należy do Ciebie −

pikolo: A czy Mógłbyś mi w tym pomóc?

===: ...to "jedź" po swoich podpunktach

===: 1. |AD|=3√5

	|BC|√3
2.		=3√5 ⇒ |BC|=2√15
	2

3. Współczynnik prostej zawierającej A i D

	6−3		1
a=		=
	5+1		2

Zatem prosta zawierająca bok BC ma równanie: y−3=−2(x+1) ⇒ y=−2x+1 4. Na tej prostej masz wyznaczyć punkty BC. Ich odległość od punktu D to √15 Możesz to oczywiście zrobić na kilka sposobów Ja napiszę równanie okręgu o środku w punkcie D i promieniu r=√15 i poszukam punktów przecięcia z prostą y=−2x+1 (x+1)²+(y−3)²=15 x²+2x+1+(−2x−2)²=15 x²+2x+1+4x²+8x+4−15=0 5x²+10x−10=0 x²+2x−2=0 Δ=4+8 √Δ=2√3 x₁=x_B=−1−√3 y₁=y_B=3+2√3 x₂=x_C=−1+√3 y₂=y_C=3−2√3

pikolo: Dziękuje bardzo

===: −

pikolo: A czy Mógłbyś mi powiedzieć jeszcze jakie są inne sposoby wyznaczenia punktów B i C?

Kacper: Przy pomocy wektorów można też.

===: ... a jak "dygasz" przed wektorami ... to odległością dwóch punktów od siebie

===: Punkt B=(x_B, −2x_B+1) |DB|=√15 √15=√(−1−x_B)²+(3+2x_B−1)² 15=1+2x_B+x_B²+4+8x_B+4x_B² 5x_B²+10x_B−10=0 x_B²+2x_B−2=0 itd... ... i już wiesz dlaczego pisałem równanie okręgu −

===: ... jak mocno byś się uparł .... to przez punkt A równanie pęku prostych i wybierasz z nich taką, która z prostą zawierającą B i C tworzy kąt 60^o (znasz wzór na cosinus kąta między prostymi)

Kacper: To raczej nie dla niego

===: ... a dlaczego nie ? Nie odbieraj nikomu tego co Jego − A ja też zamiast tangens kąta między prostymi napisałem cosinus −:(

pikolo: Dobra, wielkie dzięki za pomoc i wyjaśnienie

===: −