Zadanie Blue: Podstawą prostopadłościanu jest prostokąt, którego przekątne przecinają się pod kątem 30⁰. Przekątna prostopadłościanu ma długość 8 i jest nachylona do płaszczyzny podstawy pod kątem 60⁰. Oblicz pole powierzchni bocznej tego prostopadłościanu. Mi wyszło Pb = 16(√3+3), bo w podstawie jest prostokąt o bokach 2√3 i 2. Natomiast w odpowiedziach mam Pb= 48√2 o.O Dlaczego tak

Eve: oooo, mnie wyszło jak Tobie i to innym sposobem

Kacper: Blue napisz im do wydawnictwa wszystkie błędy, to cię nagrodzą

Eta:

	√6−√2		√6+√2
dp=4, H=4√3 sin15o=		, cos15o=
	4		4

a=√6+√2 , b= √6−√2 P_b= 2H(a+b)= 8√3*2√6= 48√2 [j²]

Eve: własnie zrób erratę i wydaj pod swoim nazwiskiem

Eta:

Eta: Podadzą Cię do sądu o zniesławienie

Blue: Eta, ale nadal nie rozumiem, dlaczego mój sposób był zły...

Eta: Pewnie gdzieś popełniłaś błąd rachunkowy Pokaż obliczenia ..................

Eve: matko, ja tez gdzieś, coś źle?

Eta:

Kacper:

	d
cos60o=
	8

1		d
	=		⇒ d=4
2		8

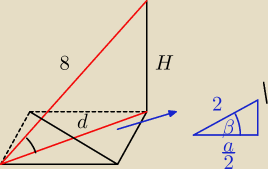
β=15^o Dalej rozwiązała Eta

Kacper: Zapomniałem o dla Ety

Blue: Ja to zrobiłam tak, że w podstawie mamy trójkąt o kątach 120, 30,30. Dzielimy go na pół, to powstanie nam trójkąt 30,60,90. Przeciwprostokątna ma 2, a więc bok ma 2√3 no i teraz już z tw. Pitagorasa: 4²= (2√3)² + x^

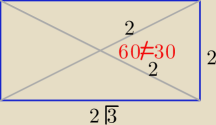
Eta: Przy Twoich obliczeniach między przekątnymi byłby kąt 60^o wniosek: sprawdź swoje rachunki

Maslanek: Kiełbasa?

Eve:

Eta: Skąd wytrzasnęłaś?120^o?

Blue: O Boże co ja zrobiłam

Eve: i juz wiem gdzie mój bład

Eta:

Blue: Już wszystko rozumiem, nie było tematu

Blue: Nie, nie Kiełbasa

Eta:

Eve: Blue to sie nazywa zmęczenie materiału

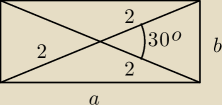
Kacper: Można też z twierdzenia cosinusów policzyć długość boków Dlaczego? Bo np. w karcie wzorów nie ma wartości dla cos15^o i sin15^o

	√3
b2=22+22−2*2*2*
	2

b²=8−4√3 b=√8−4√3 Analogicznie liczymy długość a

Blue: Można by także z Tw cosinusów?

Eta: Oczywiście Kacper

Blue: Kacper, wyprzedziłeś mnie

Eta: Teraz to już ..........."kisiel" po obiedzie

Blue: ale Kacper, co ty gadasz, że nie ma w karcie. Przecież ze wzorów można obliczyć cos(45−30)

Kacper: Wszystko można policzyć, ale nie ma podanych "gotowych" wartości To powiedz ile jest cos18^o? (to też można obliczyć )

Eta:

	√5−1
sin18o=
	4

Blue: No tego to niestety nie obliczę

Kacper: Eta zna całe tablice na pamięć

Eta: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=2018

Kacper: Takiego sposobu nie widziałem (znam sposób z podobieństwa trójkątów i jeszcze z pięciokąta jakoś się liczyło )

Mila: Pięciokąt foremny i złoty podział odcinka.

5-latek: https://matematykaszkolna.pl/forum/86984.html

Kacper: 5−latek dzięki