Geometria na płaszczyźnie
Dżepetto 18: Punkty A=(−2, −6) i B=(3, −1) są kolejnymi wierzchołkami kwadratu ABCD. Wyznacz równanie okręgu
wpisanego w ten kwadrat
30 gru 15:59
:):
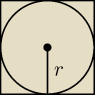
r=1/2AB
30 gru 16:03
Dżepetto 18: Mam już równanie prostej prostopadłej do AB (k)
k: x−y−4=0
prostopadła do niej l: x+y−4=0
d
AB =5
√2
Pomożecie coś więcej?
30 gru 16:24
5-latek:
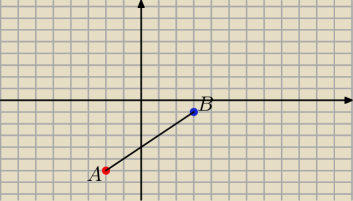
Chcialbym CI powiedziec jak tutaj jest wazny rysunek
Z niego widzisz beda tu dwa okregi.(bo beda 2 kwadraty
Mozesz pobawic sie tak np
1. Obliczyc dlugosc d odcinka |AB| −polowa odcinka |AB| to promien okregu wpisanego w
kwadrat .
2. Wyznaczyc rownanie prostej przechodzacej przez punkty A i B w postaci ogolnej (czyli
Ax+By+C
1=0
3. Wyznaczyc rownania prostych rownoleglych do prostej AB −Jest taki wzor na odleglosc dwoch
prostych o rownaniach
Ax+By+C
1=0 i Ax+By+C
2=0 a mianowicie
d juz masz policzone bo to jest dlugosc odcinka |AB|
A i B i C−1 to wspolczynniki z prostej AB musisz z tego rownania wyliczc wspolczynnik C
2
(pamietaj ze w liczniku tego wzoru jest wartosc bezwzgledna
Wyliczysz C
2 to mozesz napisac juz rownania prostych rownoleglych do AB
Teraz piszsesz rownania prostych prostopadlych do AB i przechodzcych przez punkty A i B
Obliczasz punkty przeciecia z prostymi rownoleglymi do AB i masz wspolrzedne punktow Ci C' a
takze Di D' kwadratow .
Wspolrzedne przciecia sie przekatnych tych dwoch kwadratow sobie znajdziesz (beda to
wspolrzedne srodkow okregow .
30 gru 17:14
30 gru 17:21
5-latek: Tzn wyznaczyc wspolrzedne pozostalych wierzcholkow kwadratow .
30 gru 17:22
Eta:
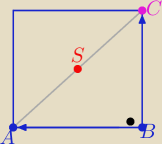
Proponuję taki sposób rozwiązania:
Najpierw wyznaczamy współrzędne punktu C
→ → → →
wykorzystując własności wektorów |AB|=|BC| i AB ⊥ BC
pomijam strzałki ( dla łatwości zapisów, a Ty je dopisz
AB=[5,5] to z warunku prostopadłości:
BC= [−5,5] ⇒ x
C−3= −5 ⋀ y
C+1=5 ⇒ C
1(−2,4)
lub BC= [5,−5] ⇒ x
C−3=5 ⋀ y
C+1= −5 ⇒ C
2(8,−6)
A teraz już sam dokończ ..... będą dwa takie okręgi
30 gru 17:23
5-latek: Dobry wieczor
Eta 
Pozdrawiam i
30 gru 17:27
Eta:
Witam
30 gru 17:29
Dżepetto 18: Zatem mając C1 i C2 wyznaczamy środki tych prostych AC1 AC2 i podstawiamy do wzoru (x−a)2
+ (y−b)2 = r2? Dobrze myślę czy się mylę? ;>
30 gru 18:07
5-latek: Dobrze myslisz
30 gru 18:09
Dżepetto 18: Uff, zatem dziękuję zarówno Tobie jak i Ecie.
Po tym zadaniu ogłaszam u mnie dobicie dziennego limitu zadań. Miłego wieczoru!
30 gru 18:13
5-latek:
30 gru 18:14