Stereometria
Blue: Mam dwa zadanka− jedno nie wiem, jak ruszyć, drugie − robię źle.
zad.1 Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami prostokątnymi. Oblicz
stosunek objętości tego ostrosłupa do objętości kuli na nim opisanej.
zad.2 Prostopadłościan ma 8 krawędzi długości x cm i 4 krawędzie długości 2x cm. Oblicz
największą możliwą objętość takiego prostopadłościanu, jeśli jest on zawarty w półkuli o
promieniu 15 cm.
| | x√2 | |
Ja to robiłam tak : ( |
| )2 + (2x)2= 152 |
| | 2 | |
Jak to zrobić?

21 gru 14:21
Kacper:
Zaraz stworzę rysunki.
21 gru 14:29
Kacper:
Zadanie z kulą nie jest łatwe. Trzeba sobie najpierw obliczyć jak wyglada ten ostrosłup
wpisany.
21 gru 15:10
===:

21 gru 15:17
21 gru 16:05
Blue: Kacper, pokazuje mi się błąd na tej stronie..
21 gru 16:46
Mila:
Masz dobry rysunek Tadeusza.
21 gru 17:15
Kacper:
Blue zapewne nie działa ci Java

21 gru 17:30
razor: też mam błąd i nie jest to spowodowane brakiem Javy

21 gru 17:31
21 gru 18:04
Blue: Kacper, niby wczytała mi się ta strona, ale rysunku nie widzę ...

21 gru 18:21
Blue: Mila a kąt prosty w tym pierwszym jest przy wierzchołku ostrosłupa

21 gru 18:22
Kacper:
Blue to przyjdź do mnie

U mnie na 3 komputerach działa

21 gru 18:22
Blue: tzn kąt prosty w ścianie bocznej
21 gru 18:22
Blue: albo nie Mila, niech ktokolwiek odpowie

21 gru 18:23
Kacper:

21 gru 18:23
===:
1. Wiedząc, że ściana boczna to trójkąt prostokątny wyznaczasz krawędź boczną
( w zależności od boku podstawy a)
2. Znasz położenie spodka wysokości ostrosłupa ... Pitagoraskiem wyznaczysz h
3. Wyrażasz V
ostrosłupa w zależności od a
4. Wyznaczasz R kuli i jej objętość
5. Pozostaje ... to co pozostaje −

21 gru 18:33
Blue: | | √3 | |
To pierwsze wyszło mi ^^ − |
| |
| | 9π | |
21 gru 18:37
Blue: Tadeusz, nie musiałeś pisać instrukcji, zorientowałam się, o co chodzi

21 gru 18:38
Blue: Największy problem to zawsze jest rysunek.
21 gru 18:39
Kacper:
Nadal nic nie widać?
21 gru 18:40
Mila:
1) Nie masz odpowiedzi?
Też mam taki wynik.
21 gru 18:46
Mila:
1) Uwaga:
Ze względu na to, że ściany boczne są Δ prostokątnymi równoramiennymi, to krawędź boczna
oznaczyłam literą a. Łatwo obliczyłam V
o. ("postawiłam "ostrosłup na ściance bocznej).
Dalej jak sugeruje kolega.
21 gru 18:50
Blue: Mam do tego akurat

21 gru 18:52
Blue: | | 2 | |
Ja liczyłam po prostu z Pitagorasa (R−H)2+( |
| hΔ)2= R2 |
| | 3 | |
21 gru 18:54
Blue: Kacper w tym Twoim linku to ja nic nie widzę.
21 gru 18:54
Mila:
Zgadza się.
21 gru 18:55
Blue: no to teraz czekam na propozycje do 2 zadanka

21 gru 18:55
21 gru 18:58
Mila:
W prawd. Kacper Ci podpowiada.Zostawiam Wam samodzielność.(Gdzie kucharek sześć...)
Zadanie 2) Jaki masz problem? i jaka jest odpowiedź?
21 gru 19:01
Blue: 2000 cm3. Problem mam ogólnie z wszystkim
21 gru 19:04
Blue: i wszyscy gdzieś uciekli

21 gru 19:38
Mila:
Czas kolacji. Zaraz zobaczę, jak to drugie zadanie się rozwiązuje.
21 gru 19:47
===:
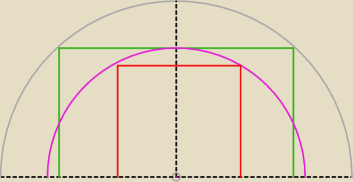
21 gru 20:20
Mila:
2) Dobrze zaczęłaś, oblicz x i objętość.
Rozważ przypadek, gdy prostopadłościan stoi na prostokącie o wymiarach x i 2x a krawędzie
boczne będą miały dł. x.
21 gru 20:30
===:

21 gru 20:43
Blue: Ahaaa, czyli chodzi o to, że podstawą jest prostokąt o wymiarach x i 2x i twierdzenie
Pitagorasa będzie wyglądać tak:
| | x√5 | |
152= ( |
| ) 2 + x 2  |
| | 2 | |
21 gru 22:25
Blue: Dzięki Mila

21 gru 22:26
Mila:
Porównujesz wyniki i wybierasz właściwą opcję.
21 gru 22:48


 http://tube.geogebra.org/student/m421753
http://tube.geogebra.org/student/m421753


 http://tube.geogebra.org/student/mqa0KH6Jt
http://tube.geogebra.org/student/mqa0KH6Jt


 U mnie na 3 komputerach działa
U mnie na 3 komputerach działa 







 https://matematykaszkolna.pl/forum/271332.html
https://matematykaszkolna.pl/forum/271332.html




