łańcuszek olimpijski
panpawel: Rozgrzewka przed OM−geometria
Jakoż, że forum matematyka.pl umarło, to może zróbmy go tutaj.
Polega to na tym, że wrzucamy rozwiązania zadania i następne zadanie do rozwiązania
Poziom Liceum
21 gru 12:13
MIXI: Jak to umarło? Dlaczego?
21 gru 12:15
J:
a czumu to forum upadło..?
21 gru 12:15
panpawel:
Zadanie 1
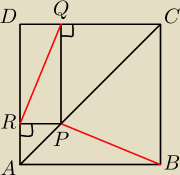
1. Punkt P leży na przekątnej AC kwadratu ABCD
Punkty Q i R są rzutami prostokątnymi punktu P odpowiednio
na proste CD i DA. Wykazać, że BP = RQ.
21 gru 12:16
Saizou :
może takie rozgrzewkowe : Udowodnij twierdzenie Ptolemeusza
"W dowolnym czworokącie ABCD wpisanym w okrąg iloczyn długości przekątnych równy jest sumie
iloczynów długości przeciwległych boków."
21 gru 12:17
21 gru 12:20
panpawel: Zignoruj mój post. Zapomnij o nim.
21 gru 12:26
Kacper:
Też jestem ciekaw co z forum matematyka.pl
21 gru 14:20
zombi: Zadanie z Pompego o ile dobrze pamiętam, ale ja z geometrii noga jestem, więc nie wcinam się w
temat

21 gru 14:37
zombi: Tak, teraz patrze to można to chyba zrobić tak, że z punktu P rzutujemy punkt T na odcinek AB
(prostopadle oczywiście) i pokazujemy, że △PRQ ≡ △PTB. Ale to luźne spostrzeżenie, być może
fałszywe.
21 gru 14:45
Saizou :
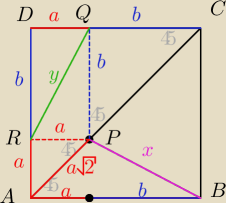
y=
√a2+b2
x
2=(a
√2)
2+(a+b)
2−2a
√2(a+b)cos45=a
2+b
2
x=
√a2+b2, zatem x=y
21 gru 14:52
zombi: Ew. tak jak ja chciałem. Wykorzystam Saizou twoje oznaczenia

Skoro |DQ| = a, to |RP| = a oraz ∡RAP = 45
o, natomiast ∡ARP = 90
o, wnioskujemy, że
|RA| = |PT| (T to ta kropeczka na rysunku Saizou na boku AB), podobnie pokazujemy, że jeśli
|QC| = |QP| = b i QC ∥ BT stąd wniosek, że |BT| = b. Ponadto ∡PTB = ∡QPR, więc
△RQP ≡ △PTB (bkb) wniosek...
21 gru 15:02
Eta:

Wystarczy zauważyć trójkąty przystające z cechy (b,k,b)
i teza gotowa

21 gru 16:46
Saizou :
Zadanie 2
Udowodnij wzór Bineta na n−tą liczbę ciągu Fibonacciego
| | 1 | | 1+√5 | | 1 | | 1−√5 | |
Fn= |
| ( |
| )n− |
| ( |
| )n |
| | √5 | | 2 | | √5 | | 2 | |
21 gru 21:15
Saizou : oczwieść gdzie n przecina zbiór liczb naturalnych
21 gru 21:16
panpawel: No świetnie. Zakładam, że to jakiś syf. Miała być rozgrzewka z geometrii.
21 gru 21:30
Saizou :
nie żadne syf, zwykła indukcja
21 gru 21:30
panpawel: Chcesz mi zdradzić, ile masz lat?
21 gru 21:31
Saizou : 19, jak ci to ma w czymś pomóc

21 gru 21:33
zombi: Z Fibonacciego jeszcze takie mam, wczoraj robiłem.
Wykaż, że (Fn,Fm) = F(n,m), gdzie (a,b) = NWD(a,b).
21 gru 22:04
Saizou :
zombi miałem takie zadanko na kolokwium z algebry

21 gru 22:07
zombi: O kurczę, to ładny poziom, bo w sumie zadanie mega proste nie jest

21 gru 22:10
Saizou :
ja raczej się boję sesji z analizy, trzeba się zacząć uczyć po świętach
21 gru 22:14
zombi: U ciebie też analiza najmocniejszym przedmiotem? Akurat o analizę ja się nie boję wcale

21 gru 22:22
Saizou :
a ja wręcz odwrotnie

twierdzenie−dowód−lemat−dowód−wniosek−dowód−twierdzenie−definicja−lemat−dowód i tak w kółko,
jest to taka grupa cykliczna

21 gru 22:57
zombi: A to w wykładach to chyba norma.

Mój wykładowca z analizy za to uwielbia robić wycieczki w
inne działy głównie w topologie, teorie miary i tym podobne rzeczy, chyba myśli że na 1 roku
rozumiemy wszystko

21 gru 23:04
Saizou :
ja mam takiego ćwiczeniowca że jak sam nie zrozumiesz to ci nie wytłumaczy, na szczęście są
dyżury i się chodzi do innych

21 gru 23:07
Wesoła: Skoro OM −geometria to
Nr1. Niech a,b,c oznaczaja dlugosci bokow trojkąta . R − dlugosc promienia opisanego na tym
trojkacie . Udowodij ze 3√3R >=a+b+c
Nr2. Udowodnij ze suma kątow wewnetrzych przestrzennego , nieplaskiego czworokąta jest mniejsza
niz 360 stopni .
21 gru 23:14
 Zadanie 1
1. Punkt P leży na przekątnej AC kwadratu ABCD
Punkty Q i R są rzutami prostokątnymi punktu P odpowiednio
na proste CD i DA. Wykazać, że BP = RQ.
Zadanie 1
1. Punkt P leży na przekątnej AC kwadratu ABCD
Punkty Q i R są rzutami prostokątnymi punktu P odpowiednio
na proste CD i DA. Wykazać, że BP = RQ.

 y=√a2+b2
x2=(a√2)2+(a+b)2−2a√2(a+b)cos45=a2+b2
x=√a2+b2, zatem x=y
y=√a2+b2
x2=(a√2)2+(a+b)2−2a√2(a+b)cos45=a2+b2
x=√a2+b2, zatem x=y
 Skoro |DQ| = a, to |RP| = a oraz ∡RAP = 45o, natomiast ∡ARP = 90o, wnioskujemy, że
|RA| = |PT| (T to ta kropeczka na rysunku Saizou na boku AB), podobnie pokazujemy, że jeśli
|QC| = |QP| = b i QC ∥ BT stąd wniosek, że |BT| = b. Ponadto ∡PTB = ∡QPR, więc
△RQP ≡ △PTB (bkb) wniosek...
Skoro |DQ| = a, to |RP| = a oraz ∡RAP = 45o, natomiast ∡ARP = 90o, wnioskujemy, że
|RA| = |PT| (T to ta kropeczka na rysunku Saizou na boku AB), podobnie pokazujemy, że jeśli
|QC| = |QP| = b i QC ∥ BT stąd wniosek, że |BT| = b. Ponadto ∡PTB = ∡QPR, więc
△RQP ≡ △PTB (bkb) wniosek...
 Wystarczy zauważyć trójkąty przystające z cechy (b,k,b)
i teza gotowa
Wystarczy zauważyć trójkąty przystające z cechy (b,k,b)
i teza gotowa 




 twierdzenie−dowód−lemat−dowód−wniosek−dowód−twierdzenie−definicja−lemat−dowód i tak w kółko,
jest to taka grupa cykliczna
twierdzenie−dowód−lemat−dowód−wniosek−dowód−twierdzenie−definicja−lemat−dowód i tak w kółko,
jest to taka grupa cykliczna 
 Mój wykładowca z analizy za to uwielbia robić wycieczki w
inne działy głównie w topologie, teorie miary i tym podobne rzeczy, chyba myśli że na 1 roku
rozumiemy wszystko
Mój wykładowca z analizy za to uwielbia robić wycieczki w
inne działy głównie w topologie, teorie miary i tym podobne rzeczy, chyba myśli że na 1 roku
rozumiemy wszystko 
