zadanie
Blue: Wyznacz objętość kuli opisanej na czworościanie foremnym o krawędzi a.
Mam problem z narysowaniem tego...

20 gru 14:36
20 gru 14:45
20 gru 14:47
Blue: hm....za dużo mi to nie pomogło, nie wiem , jak będzie wyglądał ten przekrój, na którym będzie
opisany okrąg..
20 gru 14:51
panpawel: Należy znaleźć punkt równoodległy od wierzchołków.
20 gru 14:55
panpawel:

Przekrój nie wiele tutaj da, tym bardziej, że wygląda tak

20 gru 14:57
Wesoła: Klikajac na link 14:45 bedzie tam napisane −− Odwiedz strone . Radze to zrobic .
20 gru 15:17
Mila:
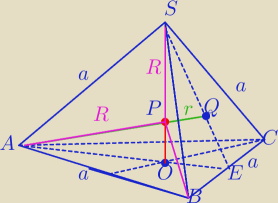
AQ= OS=H wysokości ostrosłupa
Wysokości przecinają się w stosunku 1:3 .
( Przeprowadź dowód)
P− Punkt przecięcia wysokości czworościanu= środek sfery opisanej na czworościanie.
H=U{a
√6{3}
20 gru 15:27
Wesoła: 
20 gru 15:28
20 gru 16:12
Bogdan:
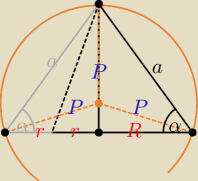
Proponuję następujące rozwiązanie:
| | 1 | |
R = |
| a√3 to długość promienia okręgu opisanego na trójkącie równobocznym |
| | 3 | |
(każda ściana czworościanu jest takim trójkątem).
P − długość promienia kuli opisanej na czworościanie foremnym
| | √3 | | 3 | | 1 | |
cosα = |
| ⇒ cos2α = |
| , sinα = √1 − cos2α = |
| √6 |
| | 3 | | 9 | | 3 | |
| | a | | 4 | |
Z twierdzenia sinusów: P = |
| , objętość kuli V = |
| P3 |
| | 2sinα | | 3 | |
20 gru 16:21
Blue: Dzięki Mila

20 gru 22:23
20 gru 22:24
Eta:
Objętość kuli V=
43πP
3 ( chochlik)

20 gru 22:58

 Przekrój nie wiele tutaj da, tym bardziej, że wygląda tak
Przekrój nie wiele tutaj da, tym bardziej, że wygląda tak 
 AQ= OS=H wysokości ostrosłupa
Wysokości przecinają się w stosunku 1:3 .
( Przeprowadź dowód)
P− Punkt przecięcia wysokości czworościanu= środek sfery opisanej na czworościanie.
H=U{a√6{3}
AQ= OS=H wysokości ostrosłupa
Wysokości przecinają się w stosunku 1:3 .
( Przeprowadź dowód)
P− Punkt przecięcia wysokości czworościanu= środek sfery opisanej na czworościanie.
H=U{a√6{3}

 Proponuję następujące rozwiązanie:
Proponuję następujące rozwiązanie:

 https://matematykaszkolna.pl/forum/271246.html
https://matematykaszkolna.pl/forum/271246.html
