zadania
Blue: Bardzo bym prosiła o sprawdzenie tych zadań , bo nie mam do nich odpowiedzi:
zad.1 a) oblicz objętość walca opisanego na sześcianie o krawędzi 6 cm.
b) Oblicz stosunek objętości walca opisanego na sześcianie do objętości walca wpisanego w ten
sześcian.
zad.2 Na stożku o tworzącej długości 6 cm i kącie rozwarcia α opisano walec. Oblicz objętość
tego walca, jeśli :
a) α= 45
0
Mi wyszło:
zad.1
a)108π
b) 2
zad.2
a) (18−9
√2)
√18+9√2π
b) 32
√5π
20 gru 11:47
panpawel:
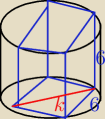
a)
k=6sqrt2
r=3sqrt2
h=6
V=18*6π=108π
20 gru 12:15
panpawel: b) dobrze
20 gru 12:17
Blue: a zadanie 2 tez jest dobrze?
20 gru 14:17
panpawel:
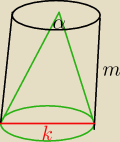
a)
k z tw. cos.
k
2=72−36
√2
k=6
√2−√2
z pitagorasa m=3
√2+√2
P=
k22π*m= zgadza się
20 gru 14:52
Blue: Jeszcze zad. 3 mam do sprawdzenia:
a) Walec o promieniu podstawy równym 1 i wysokości 4 jest wpisany w stożek o kącie rozwarcia
90
0. Oblicz objętość tego stożka.
b) Walec o promieniu podstawy równym
√3 i wysokości 2 jest wpisany w stożek o kącie rozwarcia
120
0. Oblicz pole powierzchni całkowitej tego stożka.
b) Pc= (27+18
√3)π
20 gru 14:56
Blue: chyba to 2a) mogę zostawić w takiej postaci?
20 gru 14:57
panpawel:
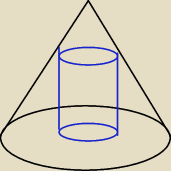
Rysunek do a) wygląda tak.
Ja miałem w święta robić olimpiadę, a nie siedzieć na forum
Później pomyślę.
20 gru 15:04
panpawel:
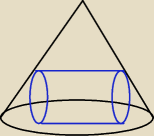
zastanawiam się , czy to też jest walec wpisany w stożek?
20 gru 15:08
Blue: Paweł, to drugie chyba nie
20 gru 15:15
panpawel: No właśnie nie wiem, bo sam nie miałem jeszcze tego w szkole, więc dobrze byłoby, gdyby ktoś z
wiedzą się wypowiedział.
20 gru 15:19
Mila:
Zadanie 3.Dobrze.
20 gru 22:39
Blue: a drugie?
20 gru 22:40
Mila:
Zadanie 2. Dobrze.
Jak liczyłaś r ?
20 gru 22:54
Blue: Z tw.cosinusów
20 gru 23:08
Mila:
Dobrze, wreszcie przekonałaś się do użyteczności tw. cosinusów.
20 gru 23:24
Blue: 
21 gru 10:41