Pomocy
szef13:
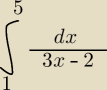
Proszę o pomoc w rozwiązaniu całki
14 gru 21:34
pomocnik: A całkę nieoznaczoną policzysz.
14 gru 21:46
14 gru 21:55
szef13: tak policze
14 gru 22:13
szef13: Wskazówki dajcie ja kto zrobić
14 gru 22:14
14 gru 23:32
Gustlik: Zawsze wywalaj to dx z licznika za ułamek, a w liczniku zostanie Ci 1 (o ile nie ma innych
czynników) i będzie to czytelniejsze.
Metoda podstawiania
| | dx | | 1 | | 1 | | 1 | | 1 | |
∫ |
| =∫ |
| dx=[ t=3x−2 ⇔ dt=3dx /:3 ⇔ dx= |
| dt ] = ∫ |
| * |
| dt= |
| | 3x−2 | | 3x−2 | | 3 | | t | | 3 | |
| | 1 | | 1 | | 1 | | 1 | |
= |
| ∫ |
| dt = |
| lnt + C = |
| ln(3x−2) + C |
| | 3 | | t | | 3 | | 3 | |
| | dx | | 1 | | 1 | |
1∫5 |
| =[ |
| ln(3x−2) ]15= |
| [ln(3*5−2)−ln(3*1−2)]= |
| | 3x−2 | | 3 | | 3 | |
| | 1 | | 1 | | 1 | |
= |
| (ln13−ln1)= |
| (ln13−0)= |
| ln13 |
| | 3 | | 3 | | 3 | |
14 gru 23:42
IQ: nie ma takiego przepisu odnośnie wywalania, poza tym z dx w liczniku jest ładniej
15 gru 16:02
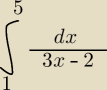 Proszę o pomoc w rozwiązaniu całki
Proszę o pomoc w rozwiązaniu całki