TRYGONOMETRIA
155178: Jak rozpisać sin4x i cos4x ? Mógłby ktoś to ładnie rozpisać, bo próbuję i nic nie wychodzi, a
pilnie tego potrzebuję ;\
13 gru 17:45
O:: sin2x=t
cos2x=1−sin2x
13 gru 17:53
Kacper:
Co to znaczy rozpisać?
13 gru 17:59
13 gru 18:04
155178: No jak zamienić to na np. sin2x ?
14 gru 00:09
sędzia:
o tej porze pilnie potrzebujesz?
14 gru 00:39
155178: Już teraz nie pilnie, ale jutro muszę zrobić 30 zadań, dlatego przy okazji to przygotowuje
sobie wzorki itp., żeby szybko to zrobić.
14 gru 01:04
sędzia:
30 zadań robi się w 30 minut, góra 60 minut
14 gru 01:11
155178: 
Powodzenia

14 gru 01:13
sędzia:
Ja robię 30 zadań w 15 minut, więc powodzenie nie jest mi w tej materii potrzebne
14 gru 01:14
sędzia:
daj jakieś zadanie
14 gru 01:15
jakubs: sędzia Dam Ci takie zadania, że przez godzinę nie zrobisz 10

14 gru 01:15
sędzia:
rozmawiam z jakimś nr, ale dawaj jakubs
14 gru 01:16
jakubs: 1.Wyznacz:
4621x ≡ 4094 mod 10799
2. Oblicz całkę:
| | sin2x*cos2x | |
∫ |
| dx |
| | sin8x+cos8x | |
3. Oblicz pole powierzchni figury ograniczonej krzywej r=sin
12φ φ ∊[0,2π]
Dawać dalej ?

14 gru 01:23
sędzia:
Tak, dalej

14 gru 01:24
jakubs: Jak zrobisz to w 15 min to masz u mnie

14 gru 01:25
sędzia:
Mam w nosie Twoje piwo
14 gru 01:26
jakubs: 
Dobranoc
14 gru 01:27
sędzia:
To są znane akademickie zadanka, szkoda mojego czasu na popisy dla nikogo, miałem
nadzieje na jakiś poważny problem, a nie zadania z kolosów. Dobranoc i mam gdzieś,
co sobie myślisz
14 gru 01:30
jakubs: Nie prosiłeś o jakieś wymagające zadania. Mogłeś sprecyzować

Gdybyś potrafił zrobić te zadania w choćby 15 min, to je byś zrobił. Te zadania może są
trywialne, ale dość czasochłonne.
14 gru 01:34
155178: Dobra to jak rozwiązać sin4x + cos4x = 1 ?
14 gru 13:51
155178: @
14 gru 14:03
155178: @@@
14 gru 14:07
155178: Dobra to jak rozwiązać sin4x + cos4x = 1 ?
14 gru 14:27
155178: Dobra to jak rozwiązać sin4x + cos4x = 1 ?
14 gru 14:43
Eta:
| | π | |
sin4x+cos4x=1 ⇒(sin2x+cos2x)2−2sin2x*cos2x=1 ⇒ ........ x= k* |
| , k∊C |
| | 2 | |
14 gru 14:47
155178: Dzięki Eta ! A co mogę zrobić z tym :
f(x)=1+sin(−x)+cos(
π2+x) wyznacz wartość parametru m f(x)=m dla którego równanie ma dwa
rozwiązania w przedziałe <π;2π>. Wiem jak zrobić to z rysunku, ale nie mam pojęcia jak
zamienić to na jedną funkcję ;\\ wiem że sin(−x)=−sinx, ale co zrobić z cos(
π2+x) ? Jak
zamienić to wszystko na jedną funkcję ?

14 gru 14:59
14 gru 15:02
Eta:
Otrzymasz : f(x)= 1−2sinx , a to już proste, jak ............

14 gru 15:04
155178: DOKŁADNIE PROSTE JAK .....

Dzięki wielkie, nie wpadłem na to

14 gru 15:11
155178: Wychodzi mi, że m∊<−1;1)u(1;3) Dobrze ?
14 gru 15:21
Eta:
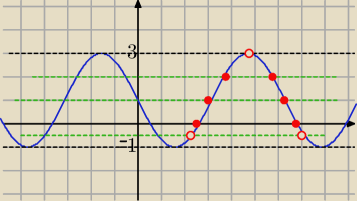
14 gru 15:36
155178: Wyznacz zbiór wartości f(x)=1+2cosx−sin
2x. Znajdz argument dla ktorego funkcja f przyjmuje
wartosc najmniejszą.
ZROBIŁEM TAK :
f(x)=1+2cosx−sin
2x=1+2cosx−1+cos
2x=cos
2x+2cosx
przeszedłem na funkcję kwadratową z pomocniczą zmienną
cosx=t
t∊<−1;1>
f(x)=t
2+2t
q=
−Δ4a=−1
Zw: y∊<−1;
∞) // ale jest to zbiór wartości funkcji z t, więc jak mogę obliczyć zbiór wartości
f(x)=cos
2x+2cosx i argument dla którego f przyjmuje wartość najmniejszą ?

14 gru 15:40
155178: Z tym wykresem jest wszystko w porządku ? Bo u mnie wyszło że 2 rozw. dla m∊<−1;1)u(1;3) bo ma
być w przedziale <−π;π>, więc dla −π = 1 czyli tam jest przerwa.
14 gru 15:51
Eta:
cosx=t to
t∊<−1,1> o tym nie możesz zapominać!
zatem g(t)= t
2+2t parabola ramionami do góry
| | −2 | |
tw= |
| = −1 to ymin= g(−1)= ..= −1 , ymax = g(1)=.... |
| | 2 | |
14 gru 15:55
Eta:
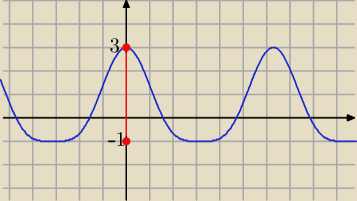
14 gru 16:01
155178: A teraz :
| | 1 | |
Oblicz cos4x jeśli sinx−cosx= |
| |
| | 3 | |
14 gru 17:13
155178: @
14 gru 17:32
155178: @@
14 gru 17:44
155178: @@@
| | 1 | |
1)Oblicz cos4x jeśli sinx−cosx= |
| |
| | 3 | |
2)Oblicz sin2x i cos2x jeśli
a)tgx=−3 x∊(
π2;π)
b)cosx=−
13 x∊(π;
32π)
14 gru 18:21
155178: @
14 gru 18:43
razor: | | 1 | |
sin2x+cos2x − 2sinxcosx = |
| |
| | 9 | |
| | 4 | |
cos4x = cos22x − sin22x = 1−2sin22x = 1−2(2sinxcosx)2 = 1 − 8(sinxcosx)2 = 1−8( |
| )2 |
| | 9 | |
= ...
14 gru 18:45
155178: A 2 ? co zmieniają mi w ogóle te przedziały ? Ćwiartki i znaki, ale nie wiem kiedy zmieniać te
znaki i jak to obliczyć ;\\
14 gru 18:46
Eta:
| | 1 | |
1/ sin2x−2sinx*cosx+cos2x= |
| |
| | 9 | |
cos(4x)= 1−2sin
2(2x)= ............
14 gru 18:50
Eta:

14 gru 18:50
155178: A co z tym 2 zadankiem ? Dzięki za pomoc z 1 .
14 gru 18:53
Eta:
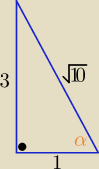
| | π | |
2/ tgα= −3 ,α∊( |
| , π) II ćw. to sinα>0 i cosα<0 |
| | 2 | |
sinα=........... , cosα=....
sin(2α)=2sinα*cosα=....
cos(2α)=cos
2α− sin
2α=.......
b) podobnie........
14 gru 18:56
 Powodzenia
Powodzenia 




 Dobranoc
Dobranoc
 Gdybyś potrafił zrobić te zadania w choćby 15 min, to je byś zrobił. Te zadania może są
trywialne, ale dość czasochłonne.
Gdybyś potrafił zrobić te zadania w choćby 15 min, to je byś zrobił. Te zadania może są
trywialne, ale dość czasochłonne.


 Dzięki wielkie, nie wpadłem na to
Dzięki wielkie, nie wpadłem na to 




