Odległość punktu od prostej Enn: Wyznacz równanie prostej do której należy punkt P(1,−1) i takiej, że odległość punktu Q(8,−2) od tej prostej wynosi 5. Ułożyłam układ 2 równań:

	|8A−2B+C|
{		=5
	√A2+B2

{A*1+B*(−1)+C=0 I nie wiem co dalej. Pomoże ktoś?

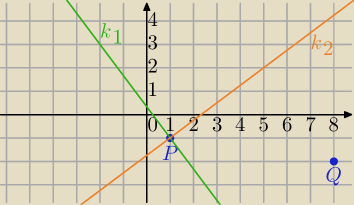
Mila: Q(8,−2) Lepiej wykorzystać postać kierunkową prostej, wtedy masz tylko jedną niewiadomą. k: y=ax+b , P(1,−1)∊k⇔−1=a+b⇔b=−1−a k: y=ax−a−1 przekształcam do postaci ogólnej k: ax−y−a−1 d=5=U{|a*8+2−a−1}{√a²+1⇔|7a+1|=5*√a²+1 /² 49a²+14a+1=25a²+25⇔

	−4		3
a=		lub a=
	3		4

	−4		1		3		7
k: y=		x+		lub k: y=		x−
	3		3		4		4

============================== Cd. Twojego sposobu A−B+C=0 C=B−A |8A−2B+B−A|=5√A²+B²⇔ |7A−B|=5√A²+B² i rozwiązuj , musisz obliczyć A w zależności od B, (lub odwrotnie) i wstawić do równania : Ax+By+B−A=0 spróbuj skończyć, to też dobry sposób

Enn: właśnie nie umiem skończyć, bo wychodzi źle

	|a*8+2−a−1|
A co do twojego sposobu to skąd wzięły się te dane: d=5=
	√a2+1

Enn: dobra wiem, nie było pytania

Enn: Bardzo Ci dziękuję

Enn: Jakbyś mogła jeszcze zerknąć na to: https://matematykaszkolna.pl/forum/270119.html