trygonometrai
IPiterek: sinxcosx=−0,5
ani ze wzoru do kwadratu też nic nie da...
9 gru 20:45
Saizou :
podpowiem że 2sinxcosx=sin2x
9 gru 20:47
Eta:
2sinx*cosx= −1
| | 3 | |
sin(2x)=−1 ⇒ 2x= |
| π+2kπ ⇒ x=...... |
| | 2 | |
9 gru 20:48
Eta:

9 gru 20:48
IPiterek: czyli pomnożyć to razy 2? wtedy 2sinxcosx=−1?
9 gru 20:49
Eta:
Tak
9 gru 20:50
IPiterek: jeszcze nie jestem peweien odczytywania z wykresów π
czemu 3/2π
9 gru 20:54
Saizou :
a dla jakiego kąta sint=−1

9 gru 20:56
9 gru 20:58
IPiterek: ok rozumiem.
a co mam zrobić przy tgx+ctgx=2
czy mam to zamienić na sin/cos i cos/sin?
9 gru 21:08
Saizou :
tg
2x−2tgx+1=0
(tgx−1)
2=0 + założenia
9 gru 21:10
Eta:
tg
2x−2tgx+1=0
(tgx−1)
2=0 ⇒ tgx=1 ⇒ x=..........
9 gru 21:10
Eta: 
9 gru 21:11
Saizou : hihihi

9 gru 21:15
Eta:

9 gru 21:16
IPiterek: ok. zaczynam ogarniać.
ale jeszcze pytanie do ostatniego.
tg=1 dla x=2/6π czyli π/3 czyli 60 stopni czyli pierwiastek z 3 ?
9 gru 21:23
Eta:
| | π | |
tgx=1 ⇒ x= |
| +k*π , k∊C |
| | 4 | |
9 gru 21:25
IPiterek: dlaczego równanie sinxctgx+cosx=2 nie ma rozwiązań?
9 gru 22:10
Kacper:
sinxctgx+cosx=2, x≠kpi
2cosx=2
cosx=1
x=kpi
Ale, oczywiście takich wartości nie możemy wstawić ze względu na dziedzinę

9 gru 22:17
IPiterek: ok
mam jeszcze takie coś: 2sin3xcos2x=0
rozumiem że sin3x=0 i cos2x=0
jak to dalej rozwiązać?
9 gru 22:27
9 gru 22:53
IPiterek: cos2x=kπ /:2
cosx=kπ/2 (a powinno do tego dojść + π/4)
9 gru 23:05
Eta:
| | π | | π | | π | |
cos2x=0 ⇒ 2x= |
| +k*π /:2 ⇒ x= |
| +k* |
| , k∊C |
| | 2 | | 4 | | 2 | |
9 gru 23:08
IPiterek: Dzięki!
sinx−cosx=0
podniosłem to do kwadratu i wyszło 1−2sinxcosx=0 czyli 1−sin2x czyli x=1/2 czyli π/6 a w
odpowiedziach pisze π/4
co zrobiłem źle?
9 gru 23:18
Eta:
| | π | |
sinx= cosx ⇒ x= |
| +k*π , k∊C |
| | 4 | |
9 gru 23:41
Eta:
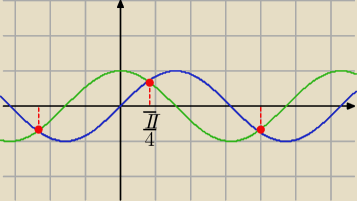
9 gru 23:44
IPiterek: ok.
kolejene zadanie sin4x + cos4x = m
dla jkaich wartości m istnieją rozwiązania
przedział się nie zmieni <−1:1> a wykres się rozciagnie tak?
10 gru 18:33






