Odległość punktu od prostej.
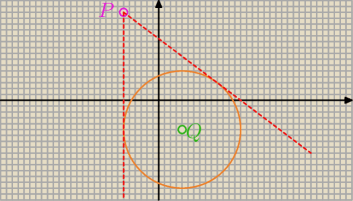
ejej: Wyznacz równanie prostej, do której należy punkt P(−6,15) i takiej, że odległość punktu Q(4,−5)
od tej prostej wynosi 10.
8 gru 22:44
Tadeusz:
.. teraz już sam/sama −
8 gru 23:01
pigor: ..., z warunków zadania prosta przez punkt P=(−6,15) :
prosta y−15= a(x+6) ⇔ (*)
ax−y+6a+15=0 − szukana prosta,
| | a*4+5+6a+15 | |
i odległość punktu Q=(4,−5) od niej to : |
| = 10 ⇔ |
| | √a2+1 | |
⇔ 10a+20=10
√a2+1 ⇔ a+2=
√a2+1 i (**)
a>−2 ⇒ (a+2)
2=a
2+1 ⇔
⇔ 4a+4=1 ⇔ 4a= −3 ⇔
a=−34 , stąd , z (**) i (*) :
−
34x−y+6*(−
34)+15=0 /*(−4) ⇔ 3x+4y+18−60=0 ⇔
⇔
3x+4y−42=0 − szukane
równanie prostej. ...
8 gru 23:17
ejej: 
8 gru 23:18
pigor: ..., o kurde no tak zapomniałem o wartości bezwzględnej
w liczniku równania odległości; przepraszam . ...
8 gru 23:19
ejej: Dzięki
8 gru 23:19
ejej: mogę jednak prosić o rozpisanie tego 2−go przypadku, bo chyba sobie z nim nie radzę
8 gru 23:32
8 gru 23:33
ejej: Tam nie ma tego, czego szukam
8 gru 23:39
ejej: zrobiłm tak:
a+2=−√a2+1
a2+4a+4=−a2−1
2a2+4a+5=0
i dalej wychodzi Δ<0, więc chyba coś niedobrze
8 gru 23:41
Mila:
Drugą prostą odczytujesz z rysunku, tam w linku masz napisane. 21 godzina
Druga prosta x=−6 nie wyjdzie Ci z tego równania.
8 gru 23:48
Tadeusz:
albo równanie okręgu = równanie pęku prostych
Wyjdą obie wartości a
9 gru 00:14
pigor: ... tu a2+4a+4= −a−1 masz bzdety ejej , a więc
z modułem byłoby np. tak :
|10a+20|=10√a2+1 ⇔ 10|a+2|=10√a2+1 ⇔ |a+2|=√a2+1 /2 , bo
obie strony dodatnie dla a≠ −2 ⇒ (a+2)2= a2+1 ⇔ a2+4a+4−a2=1 ⇔
⇔ 4a=−3 i a= −34 , a więc istnieje jedna prosta, którą wyznaczyłem o 23:17.
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
a "po bożemu" np. tak:
|a+2|=√a2+1 ⇔ (a+2>0 i a+2=√a2+1 v (a+2<0 i −(a+2)=√a2+1>0) ⇔
⇔ (a>−2 i a2+4a+4=a2+1) v (a<−2 i a2+4a+4= a2+1) ⇔
⇔ (a>−2 i a= −34) v (a<−2 i a= −34) ⇔ a= −34 v a∊∅ ⇔
⇔ a= −34 a to oznacza, ze istnieje tylko jedna prosta spełniająca
warunki zadania ...
9 gru 01:07
pigor: ... no cóż nic nie rysowałem i dlatego
nawet nie pomyślałem o tej prostej x= −6 ...
9 gru 01:14
Tadeusz:
... jeśli potraktujesz Q jako środek okręgu o promieniu 10
to te −6 samo się "narzuca" −
9 gru 01:35
pigor: ... tylko, że ja nawet przez moment nie myślałem o okręgu, bo
sądziłem, że wartość bezwzględna " załatwi" mi liczbę rozwiązań ,
dlatego jestem mocno ...
zawiedziony, że mi tego nie zapewniła ....
9 gru 01:43
Tadeusz:
... i to jest mankament tego wzoru przy stosowaniu " w drugą stronę" ....0 w mianowniku
9 gru 01:47
ejej: czyli nie da się tego obliczyć
tylko jest opcja czytania z wykresu?
9 gru 07:01
ejej: czy jest jakiś wzór na styczną, który mogę zastosowac?
9 gru 07:39
Tadeusz:
... noc nie jest najlepszą porą na matematykę −
Zmorzyła nas troszkę
tg90
o nie istniej ... trudno więc aby "wyrzuciło" ten wynik.
Można go "odnaleźć" tylko posługując się rysunkiem.
9 gru 09:49
Mila:
Dawno to napisałam, ale autorka nie czyta komentarzy.23:48
9 gru 13:47