Janek stude: @Janek zajrzy tutaj Znajdź ognisko lub kierownice i ognisko

x2		y2
	+		=1
9		4

Pokaże ktoś krok po kroku ?

Janek191: Masz już zrobione

x2		y2		x2		y2
	+		= 1 , więc z równania elipsy		+		= 1
32		22		a2		b2

mamy a² = 9 ⇒ a = 3 b² = 4 ⇒ b = 2 oraz c² = a² − b² = 3² − 2² = 9 − 4 = 5 c = √5 Ogniska elipsy: F₁ = ( c, 0) = ( √5 ; 0) F₂ = ( − c , 0) = ( −√5, 0)

stude: A mogę Cię jeszcze prosić o pomoc ?

stude: A co jak jest minus ?

	x2		y2
b)		−		=1
	4		3

	y2		x2
c)		−		=1
	3		6

Kacper: Hiperbola

stude: ale jak mam to wyznaczyć ?

Janek191: b) , c) − hiperbole Np. b)

x2		y2
	−		= 1
a2		b2

więc a² = 4 ⇒ a = 2 b² = 3 ⇒ b = √3 c² = a² + b² = 4 + 3 = 7 c = √7 Ogniska hiperboli: F₁ = ( c; 0) = ( √7 ; 0) F₂ = ( − c; 0) = ( −√7 ; 0) ======================

Janek191:

	y2		x2
c)		−		= 1
	3		6

więc b² = 3 ⇒ b = √3 a² = 6 ⇒ a = √6 c² = a² + b² = 6 + 3 = 9 c = 3 Ogniska F₁ = ( 0; c) = ( 0; 3) F₂ = ( 0; −c) = ( 0; −3)

stude: d) d) 2y²−x² = 1; e) x+1=4y² f) y²+2y−2x²=3 Proszę jeszcze o tę bo one nie są schematyczne

stude: Janek a tam jest jeszcze żeby kierownicę znaleźć

Janek191: d) 2 y² − x² = 1

y2		x2
	−		= 1
12		1

	1
b2 =		a2 = 1
	2

	1		3
c2 = a2 + b2 =		+ 1 =
	2		2

	3		√3		√6
c = √		=		=
	2		√2		2

Ogniska hiperboli: F₁ = ( 0; c) = F₂ = ( 0; − c) =

stude: ?

52: kierownice masz w parabolach czyli w e)

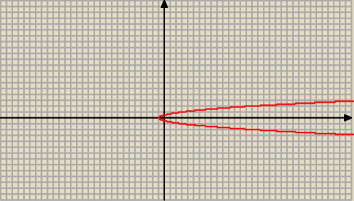
Janek191: Kierownicę ma parabola y² = 2p x Wtedy

	p
F = (		; 0) − ognisko
	2

	p
k: x = −		− równanie kierownicy
	2

−−−−−−−−−−−−−−−−−−−−−−−−−−− Pewnie będzie tak : x + 1 = 4 y² / : 4

	1		1
y2 =		x +
	4		4

więc

	1
2p =
	4

	1
p =
	8

p		1
	=
2		16

	1
Jest to parabola przesunięta o wektor [−		, 0 ]
	4

więc ognisko

	1		4		3
F = (		−		; 0) = { −		0 )
	16		16		16

kierownica

	3		1		5
k : x = −		−		= −
	16		8		16

stude: a wie ktoś jak wyznacz e i f ?

stude: up

stude: up

Janek191: e) Masz zrobione − mam nadzieję,że dobrze

stude: Tak, dziękuję Ci serdecznie ale jeszcze f ?

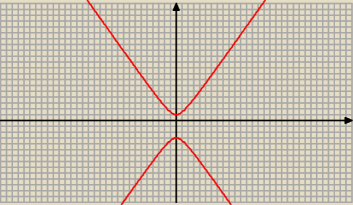
Janek191: f)

stude: ale jak wyznaczyć ogniska i kierwonice o to chodzi

stude: ?

stude: ?

stude: g ) (y+2)²=x−2; ? proszę

stude: :(

stude: Proszę o pomoc, bardzo pilne

stude: ?

stude: Ktoś coś ?

stude: :(

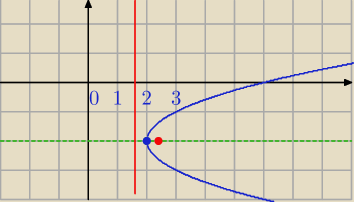
Mila: Później. g ) (y+2)²=1*(x−2); W=(2,−2) 2p=1

	1
p=
	2

p		1
	=
2		4

	1
ognisko znajduje się na osi symetrii paraboli w odległości		od W
	4

F=(2¹₄,−2) kierownica z drugiej strony W(2,−2)

	1
x=2−		=134
	4

stude: Dzięki

Mila:

stude: A ma Pani jakiś link jak wyznaczać ogniaka i kierownicę ?

Kacper: Google gryzie?

Mila: Nic dokładniejszego nie znalazłam. http://jknow.republika.pl/elipsa/elipsa.html

stude: ale to widziałem, słabe to

52: xD ja się z tego uczyłem... https://matematykaszkolna.pl/forum/265914.html

Mila: Dawniej to było w LO, tak , jak napisała Eta.