Geometria 2 Blue: zad,1 Wykaż, że punkty A=(−2,−3), B=(−3,1), C=(7,7), D=(3,0) są wierzchołkami trapezu. Oblicz długość odcinka łączącego środki ramion tego trapezu. zad.2 Punkt M jest środkiem ciężkości trójkąta równobocznego ABC, w którym A=(0,0), B=(6,0), a punkt C ma obie współrzędne dodatnie. Uzasadnij, że → → → → MA + MB +MC = 0 zad.3 Wykaż, że punkt P=(5,−4) może być wierzchołkiem kwadratu opisanego na okręgu x² +y²−4x+10y+24=0 zad.4 Dany jest czworokąt ABCD o wierzchołkach A=(0,3), B=(7,2), C=(6,−5), D=(−1,2). Wykaż, że na tym czworokącie można opisać okrąg. Moje rozwiązania: zad.1 : http://i59.tinypic.com/33ayupy.jpg http://i58.tinypic.com/2yxnrk4.jpg zad.3.: http://i58.tinypic.com/6hiy4g.jpg zad.4: http://i59.tinypic.com/zsqbt.jpg http://i62.tinypic.com/eq2z5u.jpg Nie umiem zrobić zadania 2. Proszę o pomoc i sprawdzenie moich rozwiązań.

jakubs: zad 2. Najprościej to wyznaczyć współrzędne pkt C i dalej korzystać z tego https://matematykaszkolna.pl/strona/495.html

Kacper: Zadanie 4 można tak: I − twierdzenie Ptolemeusza II − opisać okrąg na trójkącie i sprawdzić, czy pozostały wierzchołek leży na tym okręgu Twoje też może być

Kacper: Zadanie 1. Jak masz rysunek to wyznaczasz odpowiednie wektory i korzystasz z faktu, ze są równoległe (szybciej niż proste) Drugą część można ze wzoru na środek odcinka policzyć te punkty i potem raz długość odcinka Twoje też może być

Janek191: z.1 → AD = [ 3 − (−2) , 0 − (−3) ] = [ 5, 3 ] → BC = [ 7 − (−3) ; 7 − 1 ] = [ 10, 6 ] Mamy → → BC = 2* AD Wektory → → AD i BC są równoległe, więc boki AD i BC są równoległe, czyli ABCD jest trapezem.

	− 2 − 3		− 3 + 1
S1 = (		,		) = ( −2,5 ; − 1 )
	2		2

	7 + 3		7 + 0
S2 = (		,		) = ( 5 ; 3,5)
	2		2

→ S₁ S₂ = [ 5 − (−2,5) ; 3,5 − (−1)] = [ 7,5 ; 4,5 ] więc I S₁ S₂ I = √ 7,5² + 4,5² = √56,25 + 20,25 = √76,5 = 1,5√34

Kacper: Zadanie 2 Wzór na środek ciężkości trójkąta (barycentrum)

	xA+xB+xC		yA+yB+yC
S=(		,		)
	3		3

Blue: Twierdzenie Ptolemeusza − pierwsze słyszę

Kacper: Tego się nie uczy w szkole, ale jest bardzo przydatne

Blue: Kacper, a tego 2 nie da się inaczej? Wątpię, aby ten wzór był w karcie

Kacper: Blue na kolano Strona 6 karty wzorów!

Janek191: z.2 A = ( 0 ; 0) B = ( 6 ; 0) więc C = ( 3; 3√3) M − środek ciężkości , więc M = ( 3; √3 ) Policz resztę

Blue: Kacper, rzeczywiście O.o

Blue: czyli to będzie tak : → → → MA=[−3,−√3] MB= [3,−√3] MC=[0,2√3]

Blue: sorry, strzałki się głupio ułożyły

Blue: Dzięki chłopaki za pomoc z tym 2 Ale jeszcze prosiłabym o sprawdzenie 3 zadanka

Janek191: Trzeba sprawdzać na podglądzie

stude: Janek pomożesz https://matematykaszkolna.pl/forum/269520.html ?

Janek191: Już zrobione

Blue: na jakim podglądzie?

Janek191: z.3 jest ok

Janek191: @Blue Masz taki napis : zobacz podgląd

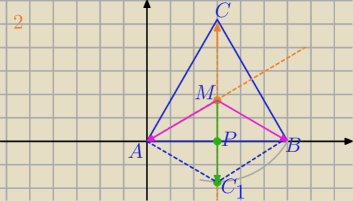
Mila: 2) MA^→+MB^→=MC₁^→ Środkowe trójkąta dzielą się w stosunku 2:1 licząc od wierzchołka kąta.

	1
|MP|=		|MC|
	2

Przekątne w równoległoboku dzielą się na połowy⇔ MC₁^→=−MC^→ ⇔MA^→+MB^→+MC^→=MC₁⁺MC^→=−MC^→+MC^→=0

Mila: ad zad 4)

	−3
cosα=
	5

	3
cosγ=		i kąty są mniejsze od 180o⇒
	5

α=180−γ⇔ α+γ=180⇔na tym czworokącie można opisać okrąg.

Blue: Mila, a to ja zapisałam tymi wektorami może być?

Mila: To znaczy wektorami o konkretnych współrzędnych? Też dobrze.

Blue: Tak, dziękuję